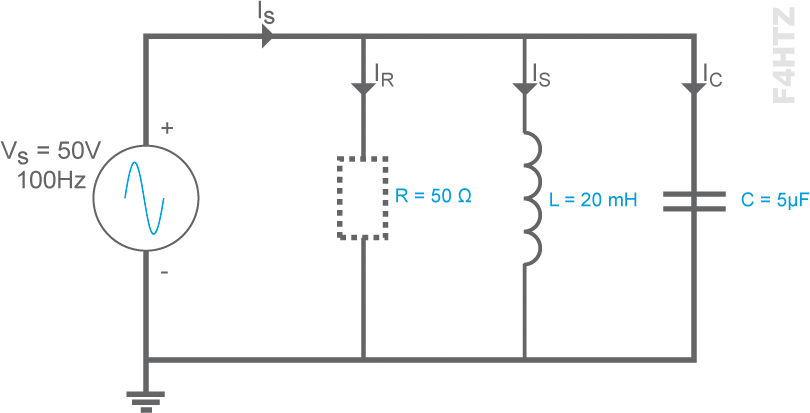
Chapitre 2
Troisième partie
Bobines et condensateurs non parfaits
- Charge, décharge et constante de temps pour les condensateurs
- Calcul de l’impédance de bobines et de condensateurs non parfaits
- Exercices

Et si après avoir étudier les bobines et les condensateurs parfaits et avoir découvert qu'il possédaient la plupart du temps, tous deux en partie, un coportement tentôt de selfique, tentôt de capacitif, nous étudions les condensteurs non parfaits ?
Charge, décharge et constante de temps pour les condensateurs
• Un condensateur se remplit (ou se charge) à travers une résistance grâce à une pile. Un inverseur permet au condensateur de se vider (ou se décharger) via la résistance.
Pour déterminer le temps de charge du condensateur, on utilise la constante de temps : t(s) = R(Ω) x C(F).
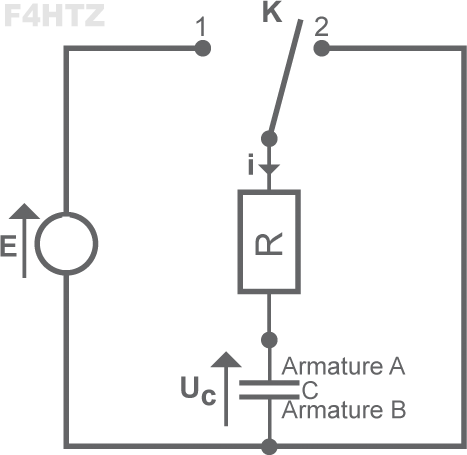
- Q = CU -> I x t = CU -> t = U/I x C = RC
- formule simplifiée : t(ms) = R(kΩ) . C(μF)
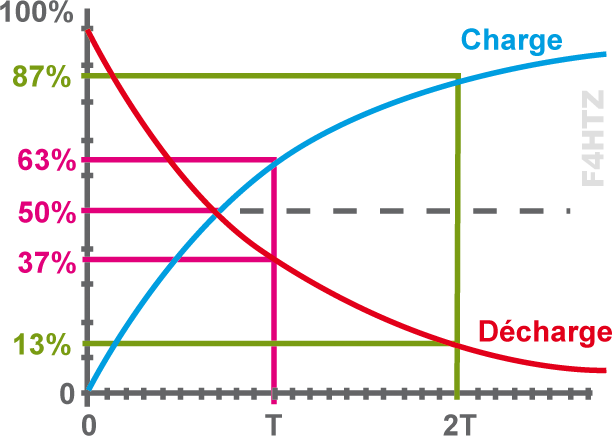
> à mesure que le condensateur se charge, la tension aux bornes de R diminue et le courant remplissant le condensateur diminue si bien qu’au bout du temps t, le condensateur n’est chargé qu’au 2/3 de la tension (63,2%).
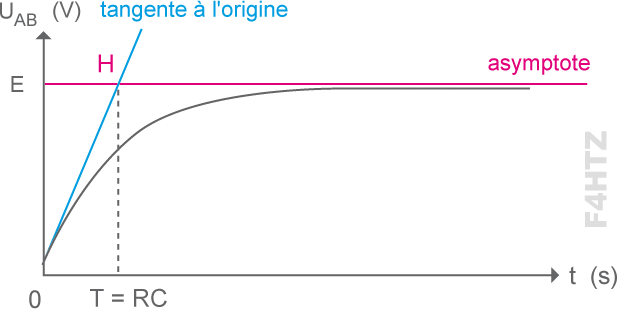
- le condensateur se remplit en 5 t
• Le raisonnement est inverse pour la décharge :
- à chaque constante de temps, le condensateur se vide du tiers (1/2,718 = 36,8%) de la tension à ses bornes.
- au bout de 1 t, il reste (1/3) x E ; au bout de 2 t, il reste (1/9) x E), etc…
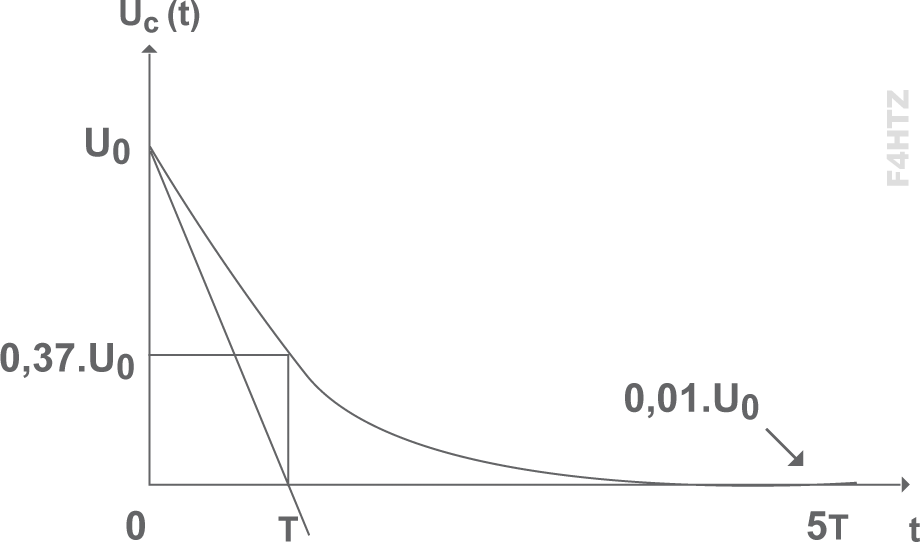
- au bout de 5 t, la tension résiduelle est inférieure à 1% de la tension d’origine : le condensateur s’est vidé.
• En théorie, le condensateur n’est jamais vide ni complètement chargé.
• L'établissement du courant dans une bobine (ou l'interruption du courant) suit la même courbe.
- la constante de temps est, dans ce cas, t(s) = L(H) / R(Ω)
> ϕ(Wb) = L x I -> U x t = L x I -> t = L x (I/U) = L/R
- Attention aux bobines des relais : lors de l'interruption brutale du courant, la tension inverse générée par le flux magnétique peut atteindre plusieurs dizaines de fois la tension d’alimentation de la bobine (ϕ = U x t).
Exemple
• Un condensateur de 100 μF se vide par l’intermédiaire d’une résistance de 8 kΩ. En combien de temps le condensateur se videra-t-il (moins de 1% de sa tension d’origine) ?
- Le condensateur sera vide au bout de 5 t :
> t(s) = R(Ω) . C(F) = 8.103 x 100.10-6 = 800.10-3 = 800 ms
> ou formule simplifiée : t(ms) = R(kΩ) . C(μF) = 8 x 100 = 800 ms
> 5t = 5 x 800 ms = 4000 ms = 4 secondes
Calcul de l’impédance de bobines et de condensateurs non parfaits
• Les bobines et les condensateurs ne sont jamais parfaits : ils ont toujours une partie résistive que nous appelons résistance pure.
• La réactance (rapport U / I) de la bobine ou du condensateur ne peut pas s’additionner avec la résistance du fil à cause du déphasage de l’intensité par rapport à la tension aux bornes de la bobine ou du condensateur.
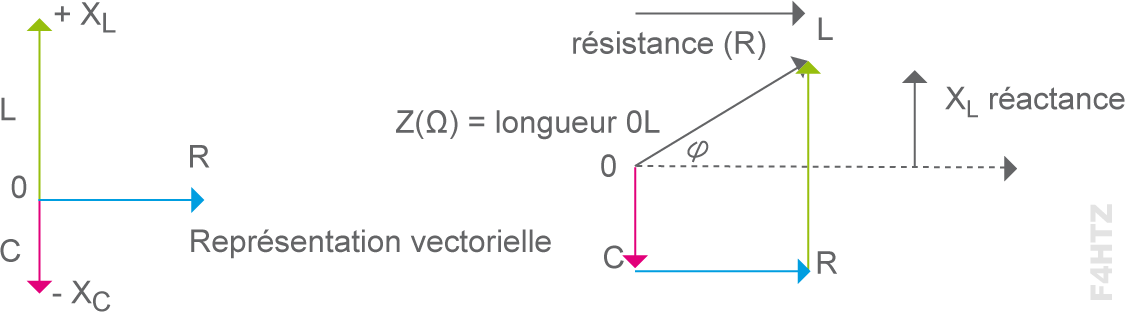
• La partie résistive s'ajoute géométriquement (somme vectorielle) à la réactance : Z = √(R² + X²)
• La direction du vecteur OZ indique le déphasage (en ° ou en fraction de π)
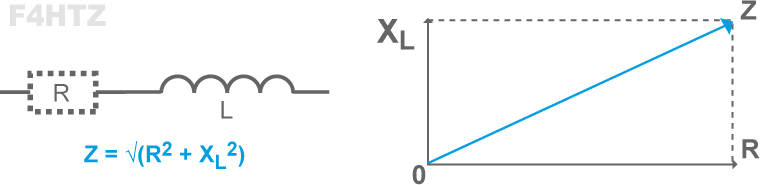
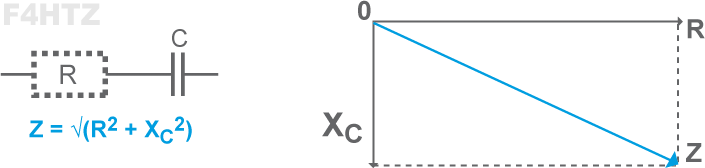
• Un condensateur a toujours une composante réactive (bobine) à cause de la forme de ses armatures (formant un coude, par exemple). Une bobine a une composante capacitive liée à l'espacement entre ses spires.
• Les vecteurs R, L, C et Z gardent la même échelle de longueur en Ω,
- le vecteur de réactance de la bobine (L) va vers le haut (+90°),
- le vecteur de la capacitance du condensateur (C) vers le bas (-90°),
- le vecteur de la résistance (R) va vers la droite (pas de déphasage)
- le vecteur d’impédance (Z) est la somme vectorielle formée :
> d’une résistance (R)
> et d’une réactance positive (+XL) ou négative (–XC)
> la résultante s’écrira sous la forme R ± jX.

• Les résistances, du fait de leur mode de fabrication, ont des composantes inductives (spirale creusée dans le matériau pour ajuster la valeur) et capacitives (les embouts des résistances).
- Les résistances de faible valeur (jusqu'à 100 Ω) ont un comportement globalement plutôt inductif
- Les résistances supérieures à 300Ω sont plutôt capacitives.
- Vers 150-200Ω, les deux effets s’annulent jusqu’à quelques GHz.
• Le rapport entre l'impédance de la bobine (ou du condensateur) et sa résistance pure détermine le déphasage entre tension et intensité mais aussi le coefficient de qualité appelé facteur Q :
- Q = Z / R = 1 / cos φ (φ = déphasage à la fréquence)
- Q exprime le rapport entre l’énergie totale emmagasinée (réactance) dans le composant et l’énergie qui sera dissipée en chaleur (résistance).
- Q dépend de la fréquence (XC et/ou XL) et de R (qui dépend aussi de la fréquence à cause de l’effet de peau du fil de la bobine)
Exemple
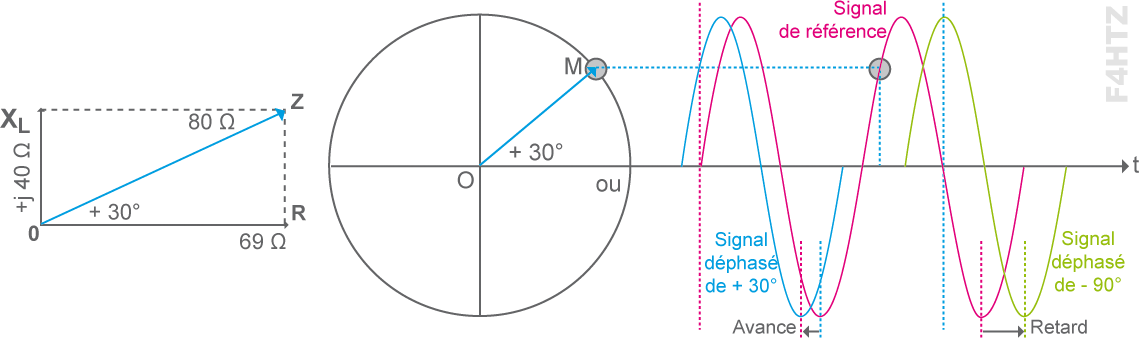
• Une bobine de 6 μH est parcourue par un courant de 1,06 MHz. La résistance pure de la bobine est de 69 Ω. Quelle est l’impédance de la bobine ? Quel est le déphasage ?
> réactance de la bobine : XL = ZL = 2πFL = 6,28 x 1,06.106 x 6.10-6 = 6,28 x 6,36 = 40 Ω
> impédance : ZL =√(R² + XL²) =√(69² + 40²) = 80 Ω
> déphasage = arctg (X / R) = tg–1 (40 / 69) = tg–1 (0,5797) = +30°
• Il résulte de ce problème de composants non parfaits des déphasages inférieurs à 90° entre la tension aux bornes du composant et l’intensité parcourue dans le composant.
• Le calcul de l’impédance (Z) permet d’appliquer la loi d’Ohm (U = Z.I). Mais, pour appliquer la loi de Joule (P = U.I), il faut tenir compte du déphasage tension/intensité (φ), ce qui amène à la formule : P = U.I.cosφ
- P = 0 si la bobine ou le condensateur sont parfaits car cos(90°) = 0
Un peu de vocabulaire (et de notions) complémentaire
• La conductance (G en Siemens) représente la faculté d'un matériau à laisser passer le courant (rappel du §1-4). Elle est l'inverse de la résistance (R en Ohms) : G = 1/R. La loi d’Ohm devient : I = U.G
• La susceptance (B en Siemens) est la réciproque de la réactance (X en Ohms) avec BL = 1/ωL et BC = ωC
• L' admittance (Y en Siemens) est la réciproque de l’impédance (Z en Ohms) avec Y = 1/Z si Z = R + jX alors Y = G – jB