Chapitre 2
Première partie
Courants alternatifs
2-1 Courants alternatifs
2-2 Valeurs maximum, efficace, moyenne, crête à crête
2-3 Un peu de pratique...

La forme la plus utilisée de courant alternatif est le courant sinusoïdal, essentiellement pour la distribution commerciale de l'énergie électrique. La fréquence utilisée est le plus souvent de 50 Hz sauf, par exemple, en Amérique du Nord où la fréquence est de 60 Hz.
2-1 Courants alternatifs
• Le courant est qualifié d’alternatif (ou périodique) si :
- il change continuellement de valeur au cours du temps
- la forme du signal se répète régulièrement
• Les courants alternatifs peuvent prendre plusieurs formes :
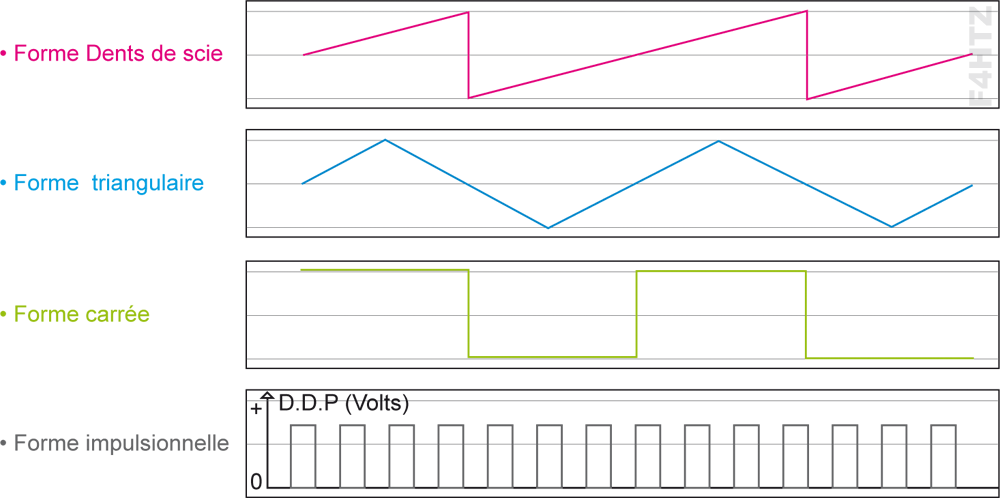
• Lorsque plusieurs courants
- Continu
- Alternatif
sont superposés, ils restent toujours alternatifs
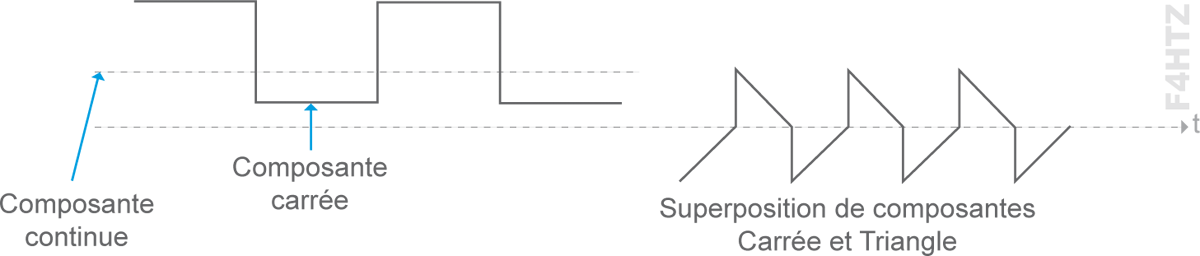
• Le signal sinusoïdal est la forme la plus régulière, sans à-coups, des signaux alternatifs
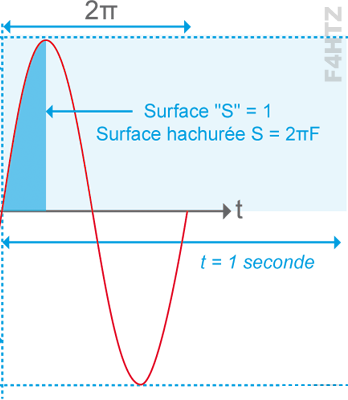
• Représentation d’une fonction Sinus
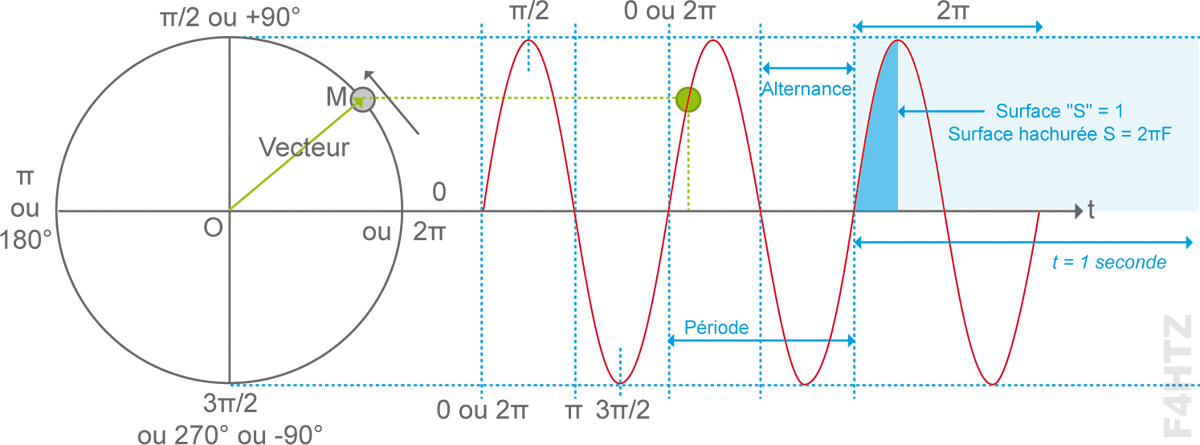
• Les formules
- durée d’une période : t(s) = 1 / F(Hz)
- fréquence : F(Hz) = 1 / t(s)
- pulsation : ω(rad/s) = 2 x π x F(Hz)
rapport entre la zone « S » (surface = 2πF pour une seconde) et la zone « s » (surface = 1)

Heinrich Rudolf Hertz (1857 - 1894)
Ingénieur et physicien allemand renommé pour avoir découvert les ondes hertziennes auxquelles il a donné son nom.
En 1877, il est étudiant à l'Institut polytechnique de Dresde avant de s'inscrire en 1878 à l'Université de Munich. Entre-temps il effectue son service militaire à Berlin.
En 1879, il est l'élève de Gustav Kirchhoff et Hermann von Helmholtz à l'Institut de physique de Berlin. Il devient maître de conférence à l'université de Kiel en 1883 où il effectue des recherches sur l'électromagnétisme.
En 1887, il réalise un oscillateur. Le 15 mars 1888, il découvre les ondes électromagnétiques dans l'air grâce à la mise au point de éclateur à sphères. À la suite de sa découverte sur les ondes hertziennes, Hertz la présente devant une assemblée d'étudiants. À la question de l'un d'entre eux qui lui demande s'il y a des applications de ces ondes, Hertz répond qu'il n'y en a aucune. l'avenir nous prouvera le contraire...
• Exemple 1 : Quelle est la pulsation d'un signal dont la fréquence est de 10 MHz ?
ω = 2 . π . F = 6,28 x 10 000 000 = 62 800 000 rad/s
• Exemple 2 : Quelle est la fréquence (en kHz) d’un signal sinusoïdal composé de 5 alternances et durant 15 μs ?
- 5 alternances forment 2,5 périodes
- 1 période dure : 15 μs / 2,5 (durée totale / nombre de période) = 6 μs
- F(MHz) = 1 / t(μs) = 0,166 MHz soit 166 kHz
Joseph Fourier (1768 - 1830)

Mathématicien et physicien français
Fourier a démontré que toute fonction périodique est la somme de fonctions sinusoïdales dont les fréquences sont multiples de la période.
Jean Baptiste Joseph Fourier est connu pour avoir déterminé, par le calcul, la diffusion de la chaleur en utilisant la décomposition d'une fonction quelconque en une série trigonométrique convergente. De telles fonctions sont appelées séries de Fourier. La méthode de calcul permettant de passer, de façon réversible, d'une fonction à la série trigonométrique correspondante est la transformation de Fourier. Cette méthode très féconde est devenue incontournable en théorie du signal, avec des applications majeures pour le traitement et la compression du son et de l'image numérique. La compression d'image JPEG, ou les normes de téléphonie 3G et 4G en découlent directement.
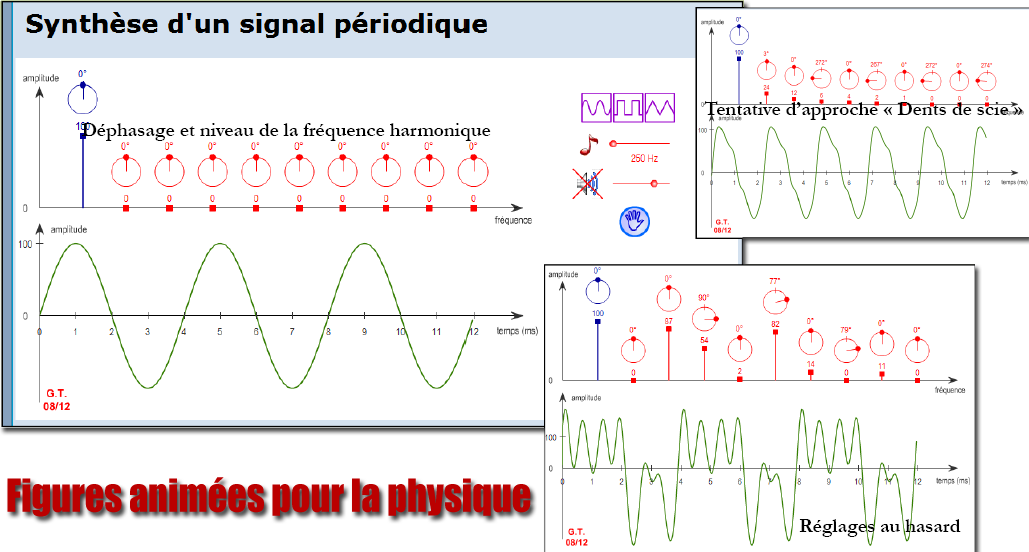
• Pour générer un signal audio à partir de sinusoïdes de fréquence multiple de la période (séries de Fourier)
• N'hésitez pas à utiliser le Site Web "Figures Animées pour la Physique" pour illustrer ce propos.)
Mise en pratique et visualisation
Remarque : changer la déphasage d’un harmonique change la forme du signal mais pas le son. Pour changer le son, il faut changer le niveau des harmoniques.
• La valeur moyenne (Umoy ou Imoy) d’un signal alternatif est la moyenne algébrique du courant ou de la tension. C’est la valeur lue par un galvanomètre. Un signal sinusoïdal a une valeur moyenne nulle.
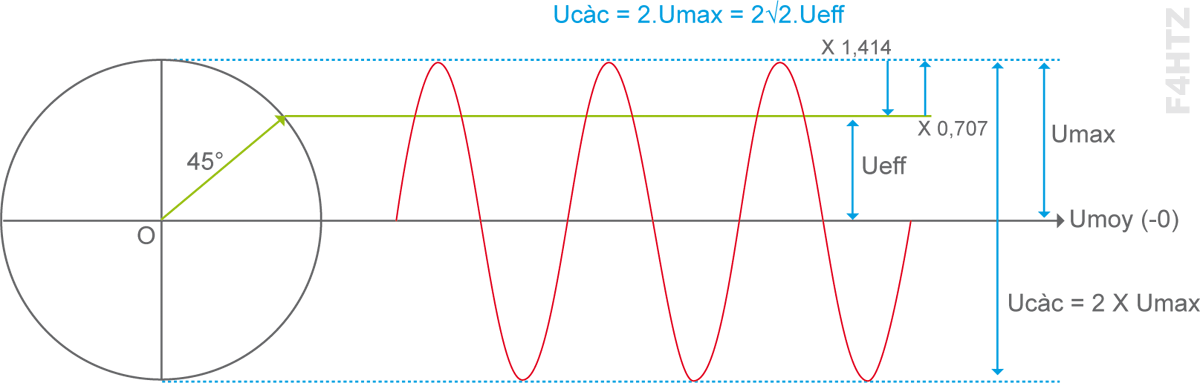
• La valeur maximale (Umax ou Imax) d’un signal alternatif est la valeur la plus grande que prend le signal au cours d’une période. Elle est appelée aussi valeur crête (Ucrête ou Icrête).
• La valeur efficace (Ueff ou Ieff) d’un signal alternatif est la valeur pour laquelle s’appliquent les lois d'Ohm et de Joule. Lorsque le signal est sinusoïdal, on a :
Umax = √2.Ueff = 1,414 x Ueff
Ueff = Umax/√2 = 0,707 x Umax.
• La valeur crête à crête (Ucàc ou Icàc) est la valeur de l’écart entre les extrêmes positif et négatif du signal.)
2-2 valeurs maximum, efficace, moyenne, crête à crête
• Seules les valeurs efficaces (Ueff et Ieff) doivent être utilisées dans les calculs en courants alternatifs sinusoïdaux.
- les lois d’Ohm et de Joule ne s’appliquent qu’avec des valeurs efficaces.
- il faut donc transformer toutes les valeurs en valeurs efficaces avant d’effectuer d’autres calculs avec les lois d’Ohm et de Joule.
• Les formules de transformation max>eff et eff>max ne fonctionnent que pour les courants sinusoïdaux.
- il existe une formule pour chaque forme de courants alternatifs.
• Exemples

Ieff = Imax X 0,707
Ieff = 1A max X 0,707
Ieff = 0,707 Aeff
U = R.I
U = 50 X 0,707 = 35,35V
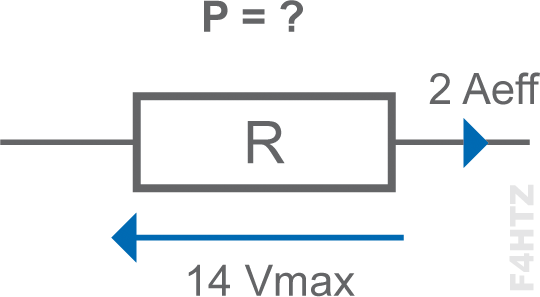
P = Ueff.Ieff
Ueff = Umax X 0,707
Ueff = 14 X 0,707 ≈ 10 Veff
P = 10V X 2A
P = 20W
• La superposition d’un signal sinusoïdal et d’une composante continue modifie la valeur efficace du signal.
- pour pouvoir appliquer la loi d’Ohm, on retiendra la formule suivante pour calculer la valeur efficace totale (Uefftot) du signal :
Uefftot = √(Ucont²+ Ueff²)
• Exemple
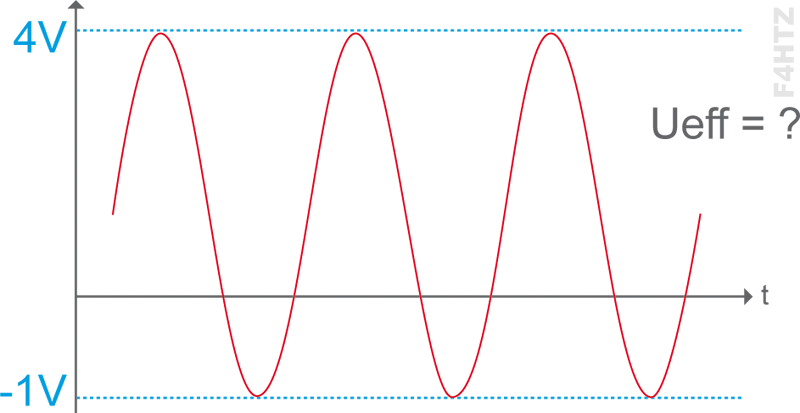
Calcul de Ueff : Ucac = 5V [= 4V –(– 1V)] donc Umax = 2,5 V ; donc Ueff = 1,77 V (= 2,5 x 0,707)
La composante continue de ce signal est égale à sa tension moyenne : Ucont = Umoy = [4 + (– 1)] / 2 = 1,5 V
Tension efficace totale : Ueff = √[1,5² + 1,77²] = 2,3 V
Remarque : si la tension continue avait été négative (-1,5 V, ce qui implique que le signal variant entre +1V et -4 V aurait été inversé), le résultat aurait été le même (heureusement !).
Lorsque deux signaux sinusoïdaux sont superposés et pour les signaux alternatifs non sinusoïdaux, le calcul se complique…
Les valeurs efficaces ne sont pas signées (+ ou – ) et on ne peut pas les additionner quand elles sont superposées (comme en courant continu).
• On rappelle que l’intensité est une "agitation organisée d’électrons" qui cheminent du – vers le + (sens électronique).
- en courant alternatif, les électrons continuent de s’agiter au rythme du courant mais ne bougent presque plus de place lorsque la fréquence augmente.
- en revanche, la propagation de l’agitation se déplace à la vitesse de la lumière (comme en courant continu) en allant de la source (le générateur) vers la charge (qui consomme l’énergie).
> la propagation de l’agitation est comparable à la chute de dominos : une fois l’impulsion donnée par la chute du premier domino, les dominos suivants chutent les uns après les autres en se déplaçant très peu alors que le mouvement de chute se propage de la première à la dernière pièce.
• Le développement des réseaux électriques au début du 20ème siècle impose le courant alternatif dont l’énergie se transporte plus facilement que celle du courant continu (débat opposant Nicolas Tesla, adepte du courant alternatif, à Thomas Edison qui milite pour le courant continu).
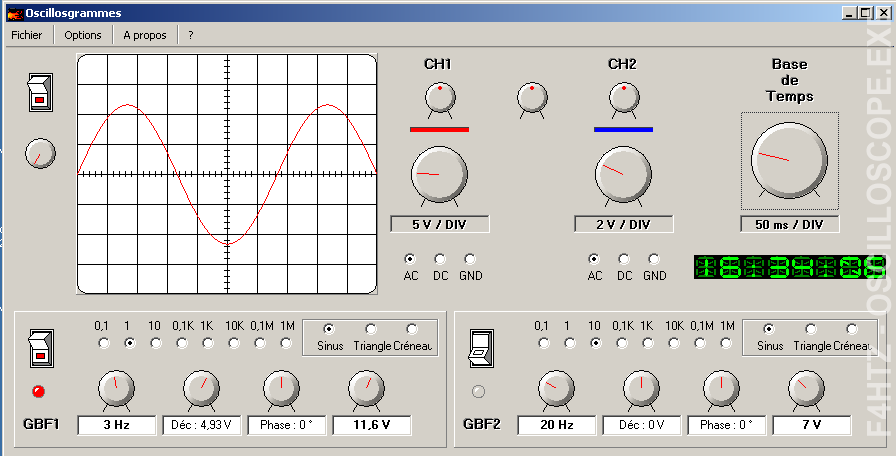
• Un oscilloscope est un instrument qui permet de visualiser sur un écran cathodique la forme d’un signal en fonction du temps.

- Le point lumineux qui parcourt l’écran représente la tension du signal et se déplace de la gauche vers la droite.
- Une sonde branchée au bout d’un câble collecte la tension à mesurer par rapport à la masse.
- Un contacteur multipositions (noté U/div) détermine la tension lue sur l’écran où sont repérées des divisions horizontales.
- Un autre contacteur (noté t/div) permet de déterminer la durée de la lecture (temps que met le point lumineux à parcourir une division de l’écran de gauche à droite).
- Les divisions verticales permettent de déterminer le temps de lecture et donc la fréquence du signal.
• Cliquez ici pour accéder au logiciel "Oscilloscope.exe".
Exemples de questions posées à l'examen
• Pulsation d'une fréquence de 1 kHz ?
- 6,28 rad/s
- 628 rad/s
- 6280 rad/s - bonne réponse
- 0,001
2 x π x F = 2 x 3,14 x 1000 = 6280 rad/s
• Fréquence d’un signal de période 500 ms ?
- 2 Hz - bonne réponse
- 2 kHz
- 0,2 Hz
- 20 Hz
500 ms = 0,5 s ; F = 1/t = 1 / 0,5 = 2 Hz
• Durée d’une période d'un signal de fréquence 2,5 MHz
- 0,4 ms
- 40 ns
- 2,5 μs
- 400 ns - bonne réponse
t = 1/ F ou t(μs) = 1 / F(MHz) = 1 / 2,5 = 0,4 μs = 400 ns (= 4 x 10-7)
Utilisez de préférence la calculette et la table de conversion pour ne pas tomber dans le piège des multiples et sous-multiples !
• Fréquence du signal ?
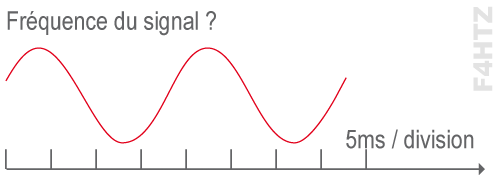
- 25 Hz
- 100 Hz
- 50 Hz
- 200 Hz - bonne réponse
la période d’observation dure : 8 x 5 ms = 40 ms, il y a 2 périodes, d’où 20 ms (ou 0,02 s) par période, d’où une fréquence de 50 Hz ( = 1 / 0,02).
• 10 V efficaces. Quelle est la tension crête ?
- 14,14 V - bonne réponse
- 7,07 V
- 28,28 V
- 20 V
Ucrête = Ueff x √2 = 10 x 1,414 = 14,14 V.
• Quelle est la valeur crête d’un signal de puissance 20 W passant dans un coaxial d’impédance de 75 Ohms ?
- 39 V
- 75 V
- 110 V
- 55 V - bonne réponse
U = √(P x R) = √(1500) ≈ 39 Volts efficaces ≈ 55 Vcrête (= 39 x 1,414 ; valeur arrondie et en supposant qu’il n’y a pas d’ondes stationnaires…)
Chapitre 2
Deuxième partie
Bobines et condensateurs parfaits
- Bobines et condensateurs
- Le condensateur
- La bobine

Après le composant Résistance dont nous avons étudié le comportement en présence de courants continus et de courants alternatifs, nous étudions deux composants qui ont des comportements particuliers en présence de courants alternatifs : la bobine et le condensateur.
Bobines et condensateurs
• Dans les formules simplifiées qui suivront, le facteur 159 est fréquemment utilisé au numérateur des fractions.
- Ce nombre correspond à une approximation de 1000 / (2 x π)
> A l’examen, on indique aussi "en retenant 1 / (2 x π) = 0,16". Dans ce cas, on utilisera les mêmes formules avec le facteur 160.
- Dans les questions de l’examen portant sur des calculs faisant intervenir le nombre π (impédance, fréquence, …), les résultats sont toujours arrondis.
Le condensateur et la bobine possèdent leurs propres caractéristiques et ont des comportements opposés mais complémentaires.

Exemples de condensateurs et de bobines
Voici quelques hommes qui sont à l'origine des phénomènes que nous allons étudier dans ce cours.

Michael Faraday est un physicien et un chimiste britannique, connu pour ses travaux fondamentaux dans le domaine de l'électromagnétisme, l'électrochimie, le diamagnétisme, et l'électrolyse. Il donne son nom à de multiples lois et phénomènes dans ces domaines, notamment la loi de Faraday (ou Lenz-Faraday) en induction électromagnétique, les lois de Faraday en électrochimie, l'effet Faraday, ou encore à des dispositifs expérimentaux comme la cage de Faraday et la cavité de Faraday.
Le farad, unité de capacité électrique, est également nommée en son honneur.

Heinrich Lenz est professeur puis recteur à l'université impériale de Saint-Pétersbourg, où il refait les expériences de Faraday. Son nom est resté attaché à la loi sur l'interaction courant électrique - champ magnétique.
Il observe en 1833 l'augmentation de la résistance des métaux avec la température et étudie l'effet Peltier.

Joseph Henry est un physicien américain qui découvrit l'auto-induction et le principe de l'induction électromagnétique des courants induits.
En 1831, il créa une unité de mesure d'induction électrique qui fut nommée le henry en son honneur. Henry expérimenta et améliora l'électroaimant, inventé en 1823 par l'Anglais William Sturgeon. Dès 1829, il avait développé des électroaimants d'une grande puissance de levée. En 1831, il fabriqua le premier télégraphe électromagnétique opérationnel. Henry conçut et construisit également l'un des premiers moteurs électriques…

Wilhelm Eduard Weber est un physicien allemand. On lui doit une théorie originale de l'interaction électromagnétique.
Docteur en 1826 de l'Académie de Berlin (1863), correspondant de l'Institut (1865), Wilhelm Eduard Weber fut professeur de physique à l'université de Göttingen.
Gauss et Weber ont publié de 1837 à 1843 les résultats des observations de la Société magnétique.
Weber a publié de 1846 à 1856 d'importantes recherches sur la détermination des forces électrodynamiques.
Rentrons maintenant dans le vif du sujet
Le condensateur
origines du phénomène
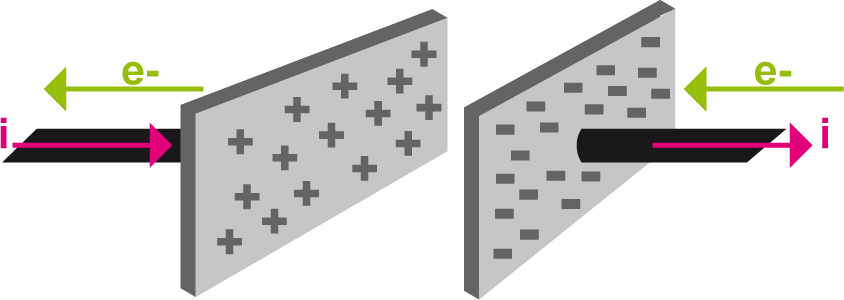
On parle de l'effet électrostatique.
Représentation schématique
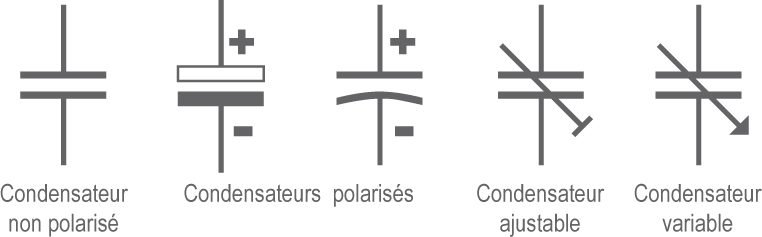
Unités : le Farad : μF, nF, pF
Capacité : C = d . S / E
C : Capacité / d :coefficient diélectrique (pour le diélectrique) / S : Surface en cm2 / E : épaisseur de la plaque en 10ème de milimètre.
calcul pratique : C(pF) = 8,85 . S (cm²) / E (1/10 mm)
- permittivité ε0 = 8,85 pF/m [= (1/36π).10-9 F/m]
- coefficient diélectrique (ou permittivité relative εr), rigidité diélectrique (en kV/mm)
Rem : ε se dit Epsilon
- condensateurs électrochimiques (polarisés)
Définitions physiques
C(F) = Q(C) / U(V) ou Q(C) = C(F) . U(V)
E(J) =½ . Q(C) . U(V)
on rappelle que Q = I x t
Code des couleurs
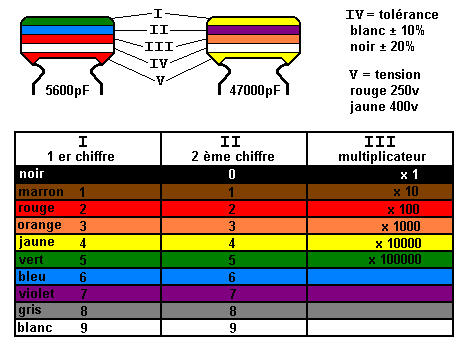
Pour les chiffres, l'odre des couleurs est exactement le même que pour les resistances.
La bobine
origines du phénomène
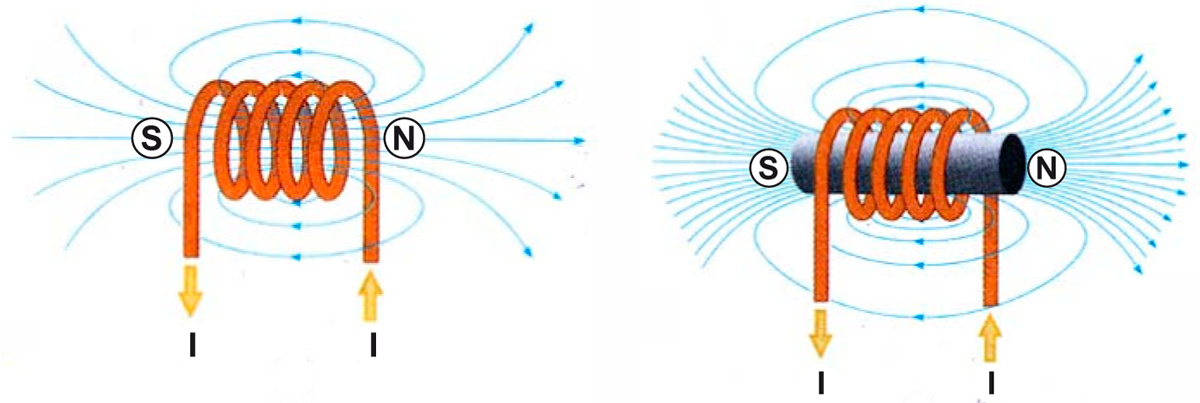
On parle de l'effet électromagnétique.
Représentation schématique

Unités : le Henry : mH, μH, nH
Inductance : L = F . N² . D² L en l’honneur de H. Lenz
Nagaoka simplifiée L(μH)=[N²xD²(cm)]/[45 D(cm)+100 long(cm)]
- formule de base : L = μo.D².N²/long
- perméabilité (μo = 1,26 μH/m [= 4π.10-7 H/m], μr (noyau)
- matériau magnétique (fer, ferrite, nickel) et diamagnétique (cuivre, zinc)
- flux d’induction magnétique (ϕ en Weber). 1 Weber est le flux d'induction magnétique qui, traversant un circuit d'une seule spire, y produit une force électromotrice de 1 volt si on l'annule en 1 seconde par une décroissance uniforme : ϕ = U x t
Rem : ϕ se dit : Fi
Définitions physiques
ϕ(Wb) = L(H) . I(A) ou L(H) = ϕ(Wb) / I(A)
E(J) = ½ L(H) . I²(A)
Comment utiliser nos lois d'Ohm et de Joule avec les condensateurs et les bobines ?
• Lorsqu’ils sont traversés par des courants alternatifs, les bobines et les condensateurs réagissent différemment :
- le condensateur ne laissera passer que la composante alternative d’une tension
- la bobine s’opposera à toutes variations de l’intensité qui la parcourt.
• Bien que ces phénomènes se mesurent en ohms, on ne peut plus parler de résistance. Le terme d’impédance (notée Z) est employé et plus précisément :
- réactance dans la cas de la bobine
- capacitance (ou réactance négative) pour le condensateur
Rem : Le therme "impédance vient de impédiment". Les impédiments sont les bagages qui ralentissent la marche d’une armée.
• Aucune énergie n’est consommée : les bobines et les condensateurs, s’ils sont parfaits, emmagasinent l’énergie puis la restituent à l’identique (pas de perte en chaleur ou dans le champ magnétique de la bobine).
Rappel : pulsation = ω (rad/s) = 2 π . F(Hz)
• Calcul de l’impédance d’un condensateur :
- Capacitance : ZC= 1 / ωC = 1 /[2 . π . F(Hz) . C(F)]
- formule simplifiée : Z(Ω) = 159 / F(MHz) / C(nF)
> C = Q / U
> C = (I x t) / U
> t / C = U / I
En cas de variation d’intensité, t = 1/2πF (partie active)
> 1 / (2πF x C) = Z
• Calcul de l’impédance d’une bobine :
- Réactance : ZL = ωL = 2 . π . F(Hz) . L(H)
- formule simplifiée : Z(Ω) = 6,28 x F(MHz) x L(μH)
> L =ϕ / I
> L = (U x t) / I
> L / t = U / I
En cas de variation de tension, t = 1/2πF (partie active)
> 2πF x L = Z
le calcul de l’impédance donné ici ne s’applique qu’à un signal sinusoïdal
Les groupements de condensateurs et de bobines
• Capacité équivalente d’un groupement de condensateurs :
- calcul inverse des résistances
- série : Ct = 1/[(1/C1) + (1/C2)] = (C1 x C2) /(C1 + C2)
Répartition de la tension au prorata inverse : le plus petit condensateur a la tension la plus élevée à ses bornes (Q = C x U et QC1 = QC2)
- parallèle : Ct= C1 + C2
• Inductance équivalente d’un groupement de bobines :
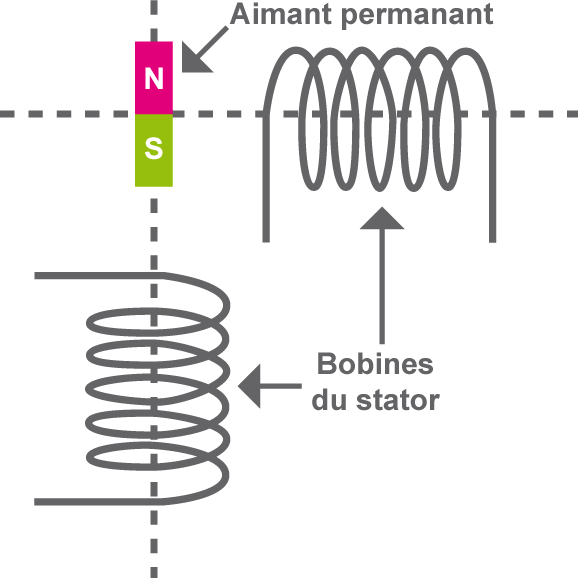
- calcul comme pour les résistances
- série : Lt = L1 + L2 ± M
M = mutuelle induction (± selon le sens des spires et valeur selon le coefficient de couplage)
- parallèle : rarement utilisé et complexe en cas de mutuelle induction
Remarque
• Dans une résistance, tension et intensité sont en phase (loi d’Ohm)
• On mesure le déphasage par rapport à l’intensité (voir tableau ci-dessous).
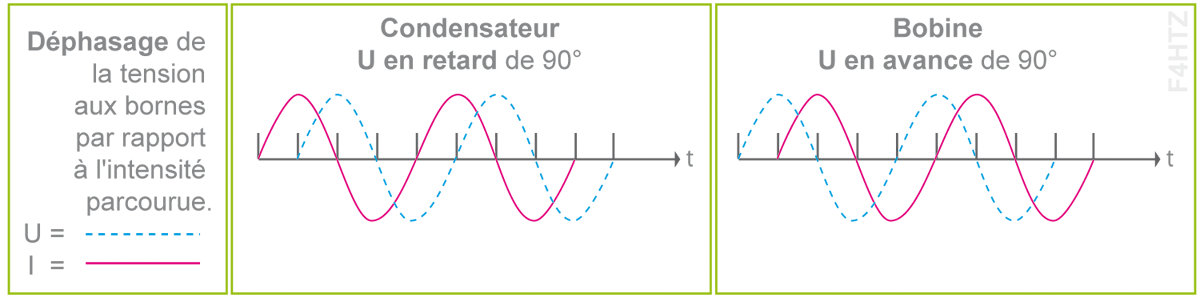
• Dans un condensateur,
- il y a d'abord établissement du courant puis établissement de la tension car le courant remplit le condensateur.
- La tension est en retard de 90° par rapport au courant.
• Dans une bobine,
- une tension est préalablement nécessaire pour générer un courant puis, une fois la réserve d’énergie créée sous la forme d’un champ magnétique, le courant s’établit.
- La tension est en avance de 90° par rapport au courant.
Mise en pratique par le calcul
• Exemple 1 : un condensateur variable a une capacité de 100 pF. Quelle sera sa valeur si la surface des lames en vis à vis est diminué de moitié ?
C = d . S / E, si S / 2 alors C / 2 donc C = 100 / 2 = 50 pF
• Exemple 2 : l’inductance d’une bobine cylindrique a une valeur de 5 μH. Cette bobine possède 40 spires. Quelle sera la valeur de l’inductance avec seulement 10 spires (en nH) ?
- L = F . N² . D² ; si N / 4 > L / 4² > L / 16 > L = 5μH / 16 = 0,3125 μH = 312,5 nH
- Remarque : dans la vraie vie, la bobine change de forme (soit elle est plus courte, soit l’espace entre les spires augmente, ce qui implique que les spires "embrassent" moins le champ magnétique qui s’échappe plus facilement). Donc, son inductance n’est pas exactement proportionnelle au carré des spires.
• Exemple 3 : Calculer Z
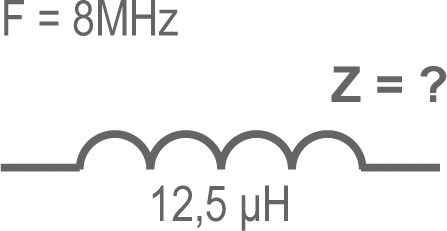 Z = ωL = 2πFL = 6,28 X 8.106 X 12,5.10-6 = 6,28 X 8 X 12,5 = 628 Ω
Z = ωL = 2πFL = 6,28 X 8.106 X 12,5.10-6 = 6,28 X 8 X 12,5 = 628 Ω
Sur une calculette :
en écriture naturelle on écrira : 2 X [π] X 8.106 (F) X 12,5.10-6 (L) = 628.100 = 628Ω
Formule simplifiée :
6,28 X 8 (F en MHz) X 12,5 (L en μH) = 628 Ω
• Exemple 4 : Quelle est la valeur du condensateur (en μF) et la quantité d'énergie (en mJ) emmagasinée dans le condensateur ?
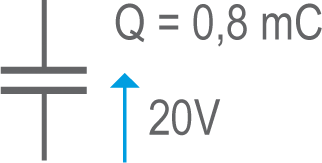 Réponse : C(F) = Q(C) / U(V) = 0,0008 / 20 = 0,00004 F = 40 μF
Réponse : C(F) = Q(C) / U(V) = 0,0008 / 20 = 0,00004 F = 40 μF
E(J) = 1/2 X Q(C) X U(V) = 1/2 X 0,0008 X 20 = 0,008 J = 8mj
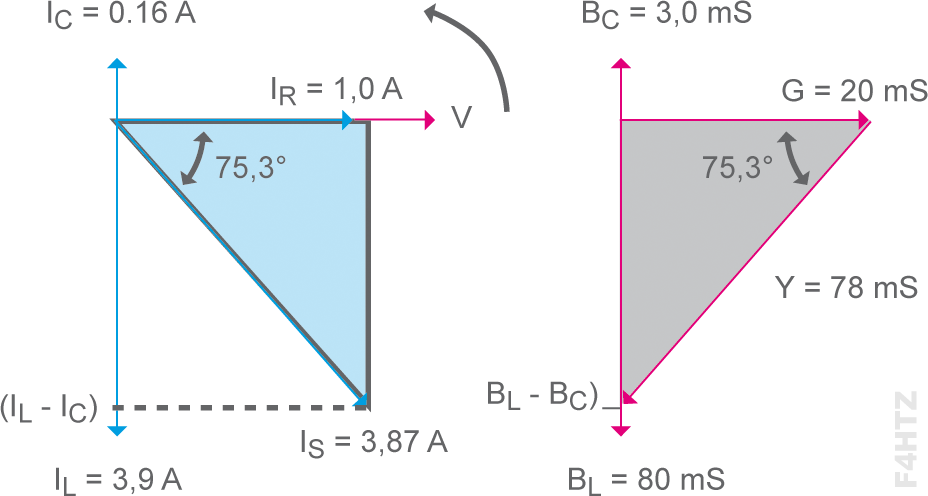
 On peut ici aussi, utiliser le système du triangle pour s'en sortir.
On peut ici aussi, utiliser le système du triangle pour s'en sortir.
• Exemple 5 : Calculer l'impédance du condensateur (en Ω)
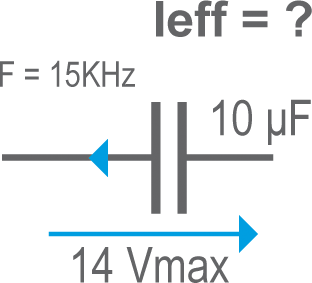 Réponse : Z = 1/(2πFC) = 1/(6,28 X 15.103 X 10.10-6) = 103/(6,28X15X10) = 1000/(6,28 x 150) ≈ 1 Ω
Réponse : Z = 1/(2πFC) = 1/(6,28 X 15.103 X 10.10-6) = 103/(6,28X15X10) = 1000/(6,28 x 150) ≈ 1 Ω
14 Vmax X 0,707 ≈ 10 Veff ; I = U / Z = 10V / 1Ω = 10 Aeff (valeur exacte = 9,33)
Sur une calculatrice, calcul de l'impédance du condensateur :
en écriture naturelle : Z = 1 / (2 X [π] X 15.103(F) X 10.10-6(C) = 1,0610.100 ≈ 1
Formule simplifiée : 159 / (F X C) = 159 / 0,015 (F en MHz) / 10000 ≈ 1
• Exemple 5 : Calculer la capacité équivalente (en pF)
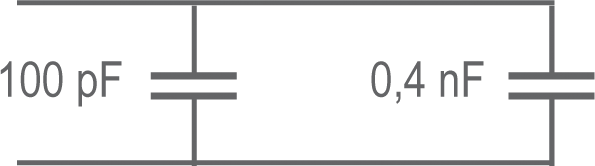 Réponse :
Réponse :
0,4 nF = 400 pF
Ct = C1 + C2 = 100 pF + 400pF = 500 pF
Chapitre 2
Troisième partie
Bobines et condensateurs non parfaits
- Charge, décharge et constante de temps pour les condensateurs
- Calcul de l’impédance de bobines et de condensateurs non parfaits
- Exercices

Et si après avoir étudier les bobines et les condensateurs parfaits et avoir découvert qu'il possédaient la plupart du temps, tous deux en partie, un coportement tentôt de selfique, tentôt de capacitif, nous étudions les condensteurs non parfaits ?
Charge, décharge et constante de temps pour les condensateurs
• Un condensateur se remplit (ou se charge) à travers une résistance grâce à une pile. Un inverseur permet au condensateur de se vider (ou se décharger) via la résistance.
Pour déterminer le temps de charge du condensateur, on utilise la constante de temps : t(s) = R(Ω) x C(F).
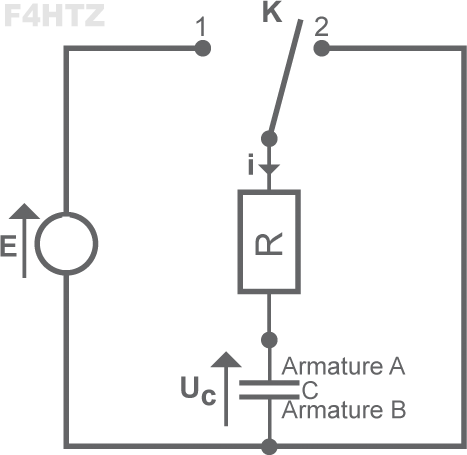
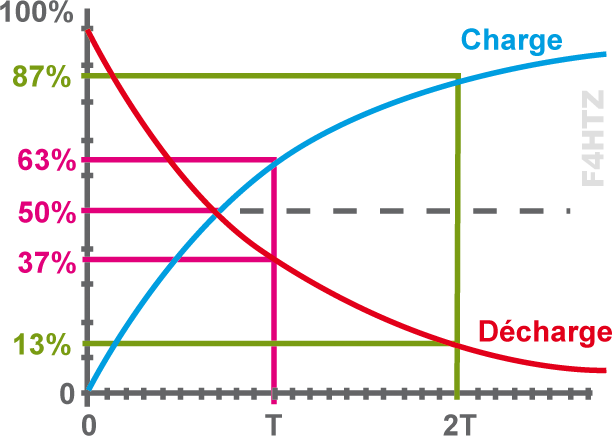
- Q = CU -> I x t = CU -> t = U/I x C = RC
- formule simplifiée : t(ms) = R(kΩ) . C(μF)
> à mesure que le condensateur se charge, la tension aux bornes de R diminue et le courant remplissant le condensateur diminue si bien qu’au bout du temps t, le condensateur n’est chargé qu’au 2/3 de la tension (63,2%).
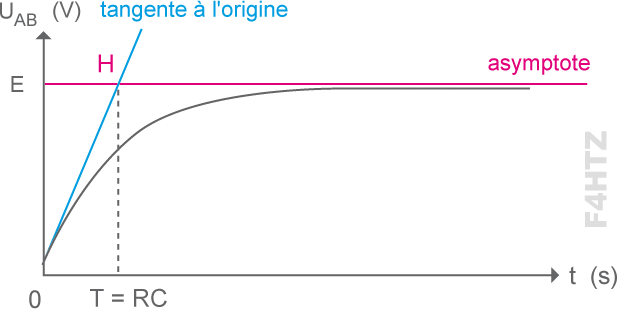
- le condensateur se remplit en 5 t
• Le raisonnement est inverse pour la décharge :
- à chaque constante de temps, le condensateur se vide du tiers (1/2,718 = 36,8%) de la tension à ses bornes.
- au bout de 1 t, il reste (1/3) x E ; au bout de 2 t, il reste (1/9) x E), etc…
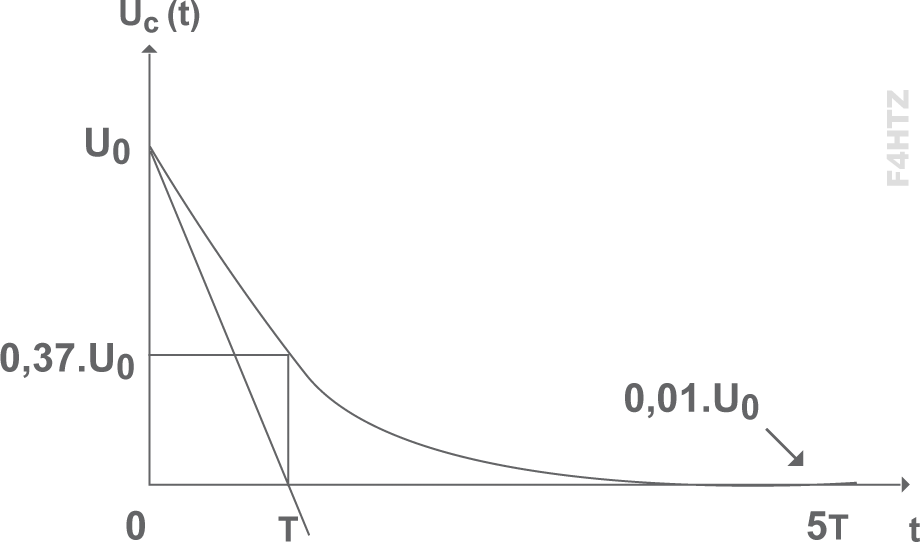
- au bout de 5 t, la tension résiduelle est inférieure à 1% de la tension d’origine : le condensateur s’est vidé.
• En théorie, le condensateur n’est jamais vide ni complètement chargé.
• L'établissement du courant dans une bobine (ou l'interruption du courant) suit la même courbe.
- la constante de temps est, dans ce cas, t(s) = L(H) / R(Ω)
> ϕ(Wb) = L x I -> U x t = L x I -> t = L x (I/U) = L/R
- Attention aux bobines des relais : lors de l'interruption brutale du courant, la tension inverse générée par le flux magnétique peut atteindre plusieurs dizaines de fois la tension d’alimentation de la bobine (ϕ = U x t).
Exemple
• Un condensateur de 100 μF se vide par l’intermédiaire d’une résistance de 8 kΩ. En combien de temps le condensateur se videra-t-il (moins de 1% de sa tension d’origine) ?
- Le condensateur sera vide au bout de 5 t :
> t(s) = R(Ω) . C(F) = 8.103 x 100.10-6 = 800.10-3 = 800 ms
> ou formule simplifiée : t(ms) = R(kΩ) . C(μF) = 8 x 100 = 800 ms
> 5t = 5 x 800 ms = 4000 ms = 4 secondes
Calcul de l’impédance de bobines et de condensateurs non parfaits
• Les bobines et les condensateurs ne sont jamais parfaits : ils ont toujours une partie résistive que nous appelons résistance pure.
• La réactance (rapport U / I) de la bobine ou du condensateur ne peut pas s’additionner avec la résistance du fil à cause du déphasage de l’intensité par rapport à la tension aux bornes de la bobine ou du condensateur.
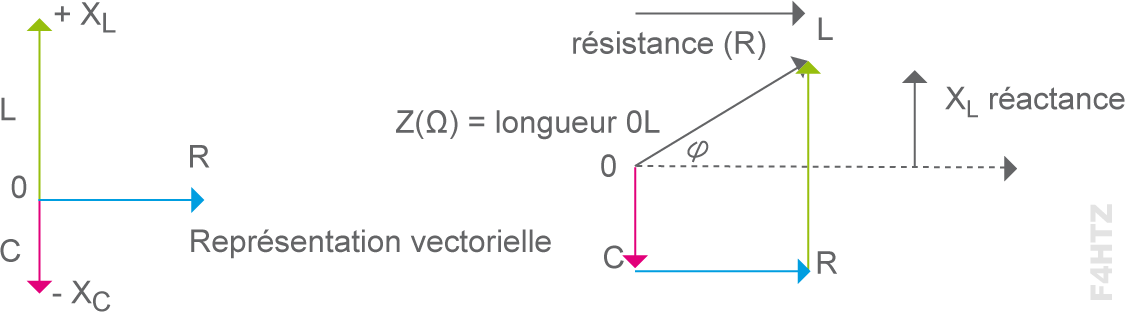
• La partie résistive s'ajoute géométriquement (somme vectorielle) à la réactance : Z = √(R² + X²)
• La direction du vecteur OZ indique le déphasage (en ° ou en fraction de π)
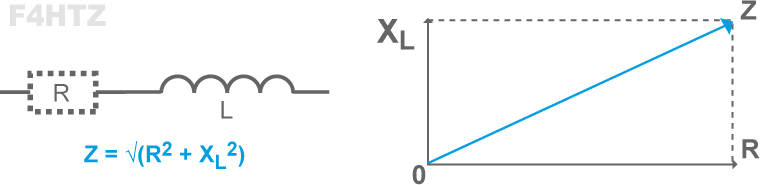
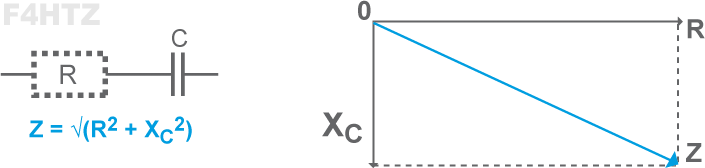
• Un condensateur a toujours une composante réactive (bobine) à cause de la forme de ses armatures (formant un coude, par exemple). Une bobine a une composante capacitive liée à l'espacement entre ses spires.
• Les vecteurs R, L, C et Z gardent la même échelle de longueur en Ω,
- le vecteur de réactance de la bobine (L) va vers le haut (+90°),
- le vecteur de la capacitance du condensateur (C) vers le bas (-90°),
- le vecteur de la résistance (R) va vers la droite (pas de déphasage)
- le vecteur d’impédance (Z) est la somme vectorielle formée :
> d’une résistance (R)
> et d’une réactance positive (+XL) ou négative (–XC)
> la résultante s’écrira sous la forme R ± jX.

• Les résistances, du fait de leur mode de fabrication, ont des composantes inductives (spirale creusée dans le matériau pour ajuster la valeur) et capacitives (les embouts des résistances).
- Les résistances de faible valeur (jusqu'à 100 Ω) ont un comportement globalement plutôt inductif
- Les résistances supérieures à 300Ω sont plutôt capacitives.
- Vers 150-200Ω, les deux effets s’annulent jusqu’à quelques GHz.
• Le rapport entre l'impédance de la bobine (ou du condensateur) et sa résistance pure détermine le déphasage entre tension et intensité mais aussi le coefficient de qualité appelé facteur Q :
- Q = Z / R = 1 / cos φ (φ = déphasage à la fréquence)
- Q exprime le rapport entre l’énergie totale emmagasinée (réactance) dans le composant et l’énergie qui sera dissipée en chaleur (résistance).
- Q dépend de la fréquence (XC et/ou XL) et de R (qui dépend aussi de la fréquence à cause de l’effet de peau du fil de la bobine)
Exemple
• Une bobine de 6 μH est parcourue par un courant de 1,06 MHz. La résistance pure de la bobine est de 69 Ω. Quelle est l’impédance de la bobine ? Quel est le déphasage ?
> réactance de la bobine : XL = ZL = 2πFL = 6,28 x 1,06.106 x 6.10-6 = 6,28 x 6,36 = 40 Ω
> impédance : ZL =√(R² + XL²) =√(69² + 40²) = 80 Ω
> déphasage = arctg (X / R) = tg–1 (40 / 69) = tg–1 (0,5797) = +30°
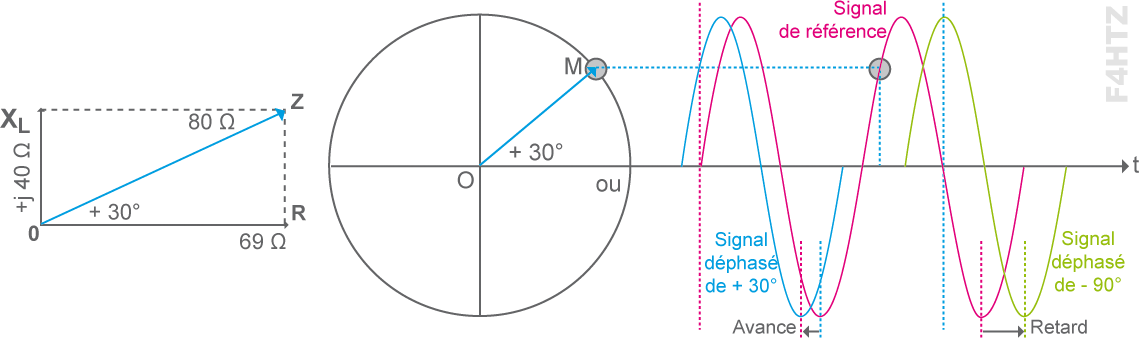
• Il résulte de ce problème de composants non parfaits des déphasages inférieurs à 90° entre la tension aux bornes du composant et l’intensité parcourue dans le composant.
• Le calcul de l’impédance (Z) permet d’appliquer la loi d’Ohm (U = Z.I). Mais, pour appliquer la loi de Joule (P = U.I), il faut tenir compte du déphasage tension/intensité (φ), ce qui amène à la formule : P = U.I.cosφ
- P = 0 si la bobine ou le condensateur sont parfaits car cos(90°) = 0
Un peu de vocabulaire (et de notions) complémentaire
• La conductance (G en Siemens) représente la faculté d'un matériau à laisser passer le courant (rappel du §1-4). Elle est l'inverse de la résistance (R en Ohms) : G = 1/R. La loi d’Ohm devient : I = U.G
• La susceptance (B en Siemens) est la réciproque de la réactance (X en Ohms) avec BL = 1/ωL et BC = ωC
• L' admittance (Y en Siemens) est la réciproque de l’impédance (Z en Ohms) avec Y = 1/Z si Z = R + jX alors Y = G – jB