Chapitre 2
Première partie
Courants alternatifs
2-1 Courants alternatifs
2-2 Valeurs maximum, efficace, moyenne, crête à crête
2-3 Un peu de pratique...

La forme la plus utilisée de courant alternatif est le courant sinusoïdal, essentiellement pour la distribution commerciale de l'énergie électrique. La fréquence utilisée est le plus souvent de 50 Hz sauf, par exemple, en Amérique du Nord où la fréquence est de 60 Hz.
2-1 Courants alternatifs
• Le courant est qualifié d’alternatif (ou périodique) si :
- il change continuellement de valeur au cours du temps
- la forme du signal se répète régulièrement
• Les courants alternatifs peuvent prendre plusieurs formes :
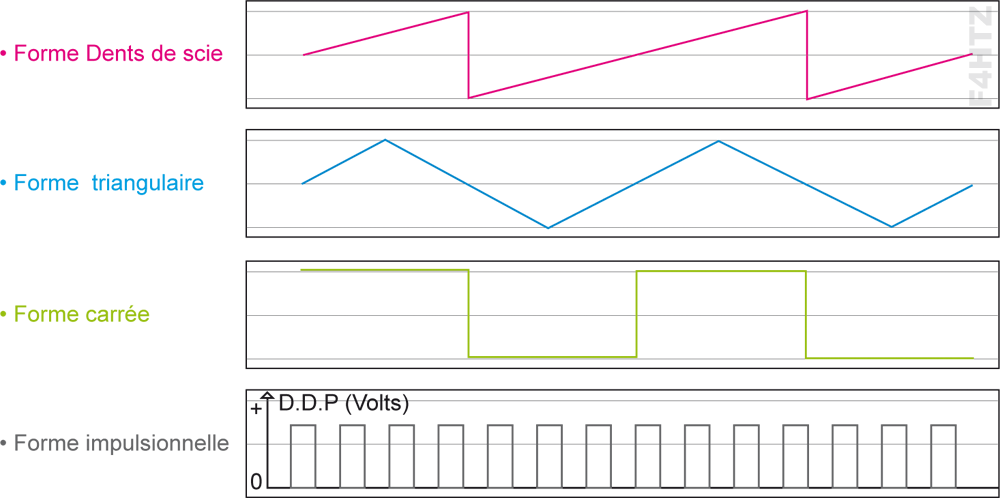
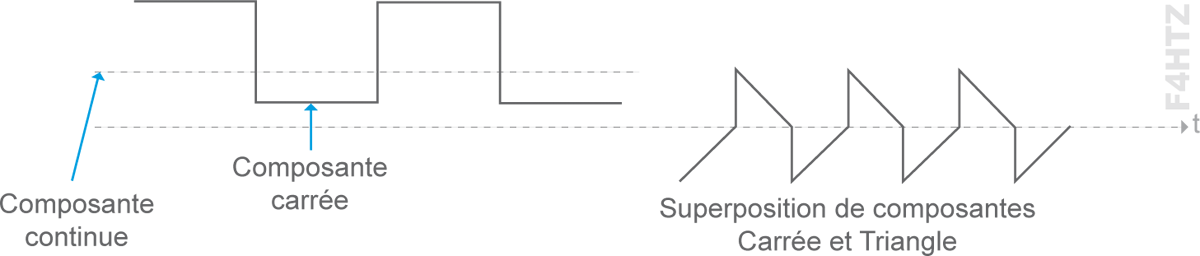
• Lorsque plusieurs courants
- Continu
- Alternatif
sont superposés, ils restent toujours alternatifs
• Le signal sinusoïdal est la forme la plus régulière, sans à-coups, des signaux alternatifs
• Représentation d’une fonction Sinus
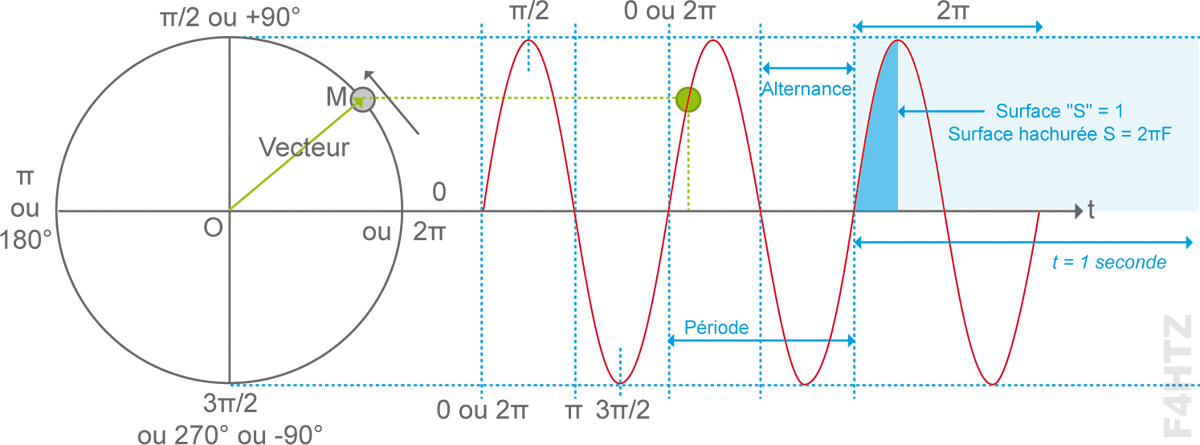
• Les formules
- durée d’une période : t(s) = 1 / F(Hz)
- fréquence : F(Hz) = 1 / t(s)
- pulsation : ω(rad/s) = 2 x π x F(Hz)
rapport entre la zone « S » (surface = 2πF pour une seconde) et la zone « s » (surface = 1)

Heinrich Rudolf Hertz (1857 - 1894)
Ingénieur et physicien allemand renommé pour avoir découvert les ondes hertziennes auxquelles il a donné son nom.
En 1877, il est étudiant à l'Institut polytechnique de Dresde avant de s'inscrire en 1878 à l'Université de Munich. Entre-temps il effectue son service militaire à Berlin.
En 1879, il est l'élève de Gustav Kirchhoff et Hermann von Helmholtz à l'Institut de physique de Berlin. Il devient maître de conférence à l'université de Kiel en 1883 où il effectue des recherches sur l'électromagnétisme.
En 1887, il réalise un oscillateur. Le 15 mars 1888, il découvre les ondes électromagnétiques dans l'air grâce à la mise au point de éclateur à sphères. À la suite de sa découverte sur les ondes hertziennes, Hertz la présente devant une assemblée d'étudiants. À la question de l'un d'entre eux qui lui demande s'il y a des applications de ces ondes, Hertz répond qu'il n'y en a aucune. l'avenir nous prouvera le contraire...
• Exemple 1 : Quelle est la pulsation d'un signal dont la fréquence est de 10 MHz ?
ω = 2 . π . F = 6,28 x 10 000 000 = 62 800 000 rad/s
• Exemple 2 : Quelle est la fréquence (en kHz) d’un signal sinusoïdal composé de 5 alternances et durant 15 μs ?
- 5 alternances forment 2,5 périodes
- 1 période dure : 15 μs / 2,5 (durée totale / nombre de période) = 6 μs
- F(MHz) = 1 / t(μs) = 0,166 MHz soit 166 kHz
Joseph Fourier (1768 - 1830)

Mathématicien et physicien français
Fourier a démontré que toute fonction périodique est la somme de fonctions sinusoïdales dont les fréquences sont multiples de la période.
Jean Baptiste Joseph Fourier est connu pour avoir déterminé, par le calcul, la diffusion de la chaleur en utilisant la décomposition d'une fonction quelconque en une série trigonométrique convergente. De telles fonctions sont appelées séries de Fourier. La méthode de calcul permettant de passer, de façon réversible, d'une fonction à la série trigonométrique correspondante est la transformation de Fourier. Cette méthode très féconde est devenue incontournable en théorie du signal, avec des applications majeures pour le traitement et la compression du son et de l'image numérique. La compression d'image JPEG, ou les normes de téléphonie 3G et 4G en découlent directement.
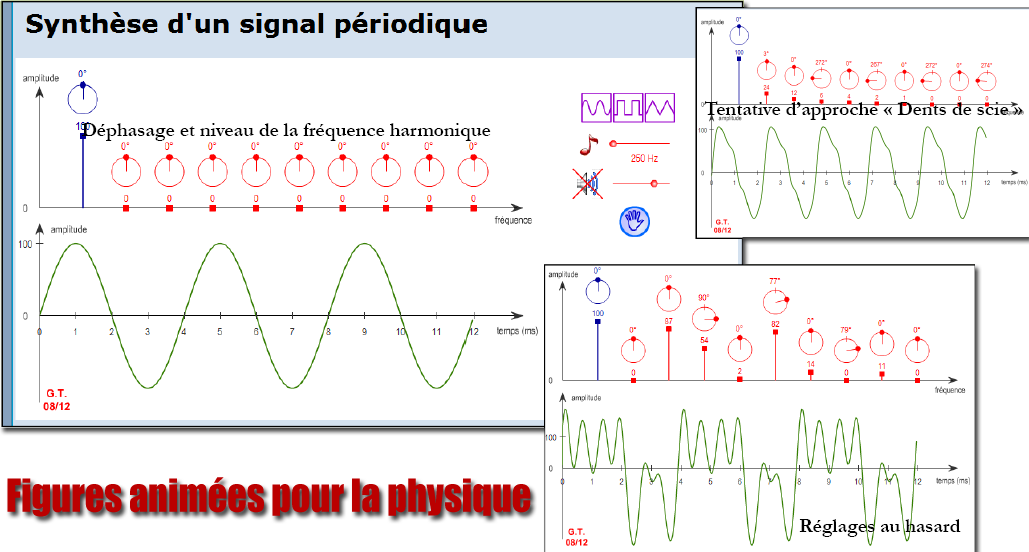
• Pour générer un signal audio à partir de sinusoïdes de fréquence multiple de la période (séries de Fourier)
• N'hésitez pas à utiliser le Site Web "Figures Animées pour la Physique" pour illustrer ce propos.)
Mise en pratique et visualisation
Remarque : changer la déphasage d’un harmonique change la forme du signal mais pas le son. Pour changer le son, il faut changer le niveau des harmoniques.
• La valeur moyenne (Umoy ou Imoy) d’un signal alternatif est la moyenne algébrique du courant ou de la tension. C’est la valeur lue par un galvanomètre. Un signal sinusoïdal a une valeur moyenne nulle.
• La valeur maximale (Umax ou Imax) d’un signal alternatif est la valeur la plus grande que prend le signal au cours d’une période. Elle est appelée aussi valeur crête (Ucrête ou Icrête).
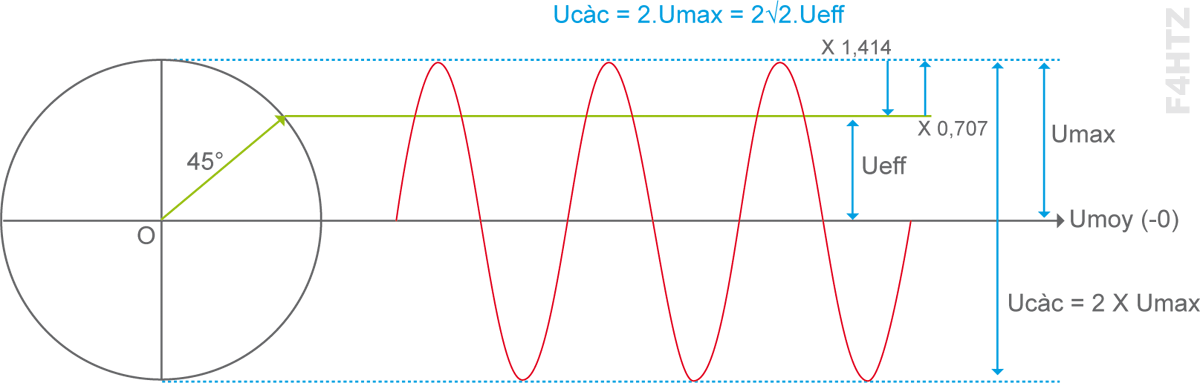
• La valeur efficace (Ueff ou Ieff) d’un signal alternatif est la valeur pour laquelle s’appliquent les lois d'Ohm et de Joule. Lorsque le signal est sinusoïdal, on a :
Umax = √2.Ueff = 1,414 x Ueff
Ueff = Umax/√2 = 0,707 x Umax.
• La valeur crête à crête (Ucàc ou Icàc) est la valeur de l’écart entre les extrêmes positif et négatif du signal.)
2-2 valeurs maximum, efficace, moyenne, crête à crête
• Seules les valeurs efficaces (Ueff et Ieff) doivent être utilisées dans les calculs en courants alternatifs sinusoïdaux.
- les lois d’Ohm et de Joule ne s’appliquent qu’avec des valeurs efficaces.
- il faut donc transformer toutes les valeurs en valeurs efficaces avant d’effectuer d’autres calculs avec les lois d’Ohm et de Joule.
• Les formules de transformation max>eff et eff>max ne fonctionnent que pour les courants sinusoïdaux.
- il existe une formule pour chaque forme de courants alternatifs.
• Exemples

Ieff = Imax X 0,707
Ieff = 1A max X 0,707
Ieff = 0,707 Aeff
U = R.I
U = 50 X 0,707 = 35,35V
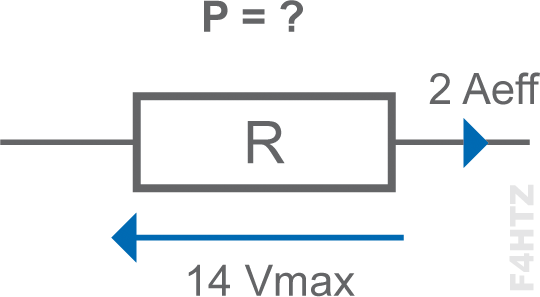
P = Ueff.Ieff
Ueff = Umax X 0,707
Ueff = 14 X 0,707 ≈ 10 Veff
P = 10V X 2A
P = 20W
• La superposition d’un signal sinusoïdal et d’une composante continue modifie la valeur efficace du signal.
- pour pouvoir appliquer la loi d’Ohm, on retiendra la formule suivante pour calculer la valeur efficace totale (Uefftot) du signal :
Uefftot = √(Ucont²+ Ueff²)
• Exemple
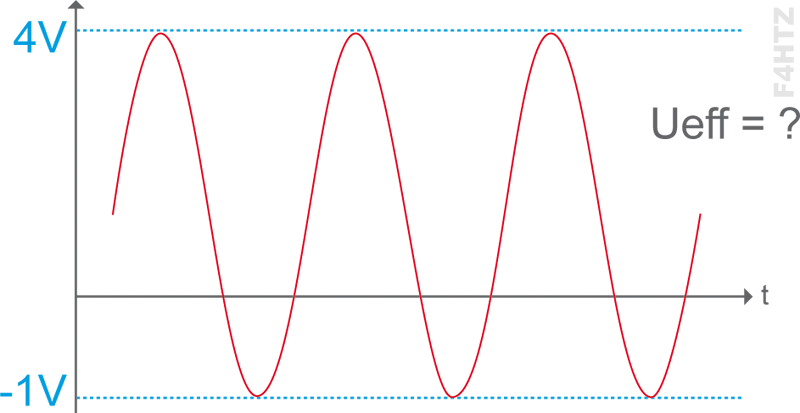
Calcul de Ueff : Ucac = 5V [= 4V –(– 1V)] donc Umax = 2,5 V ; donc Ueff = 1,77 V (= 2,5 x 0,707)
La composante continue de ce signal est égale à sa tension moyenne : Ucont = Umoy = [4 + (– 1)] / 2 = 1,5 V
Tension efficace totale : Ueff = √[1,5² + 1,77²] = 2,3 V
Remarque : si la tension continue avait été négative (-1,5 V, ce qui implique que le signal variant entre +1V et -4 V aurait été inversé), le résultat aurait été le même (heureusement !).
Lorsque deux signaux sinusoïdaux sont superposés et pour les signaux alternatifs non sinusoïdaux, le calcul se complique…
Les valeurs efficaces ne sont pas signées (+ ou – ) et on ne peut pas les additionner quand elles sont superposées (comme en courant continu).
• On rappelle que l’intensité est une "agitation organisée d’électrons" qui cheminent du – vers le + (sens électronique).
- en courant alternatif, les électrons continuent de s’agiter au rythme du courant mais ne bougent presque plus de place lorsque la fréquence augmente.
- en revanche, la propagation de l’agitation se déplace à la vitesse de la lumière (comme en courant continu) en allant de la source (le générateur) vers la charge (qui consomme l’énergie).
> la propagation de l’agitation est comparable à la chute de dominos : une fois l’impulsion donnée par la chute du premier domino, les dominos suivants chutent les uns après les autres en se déplaçant très peu alors que le mouvement de chute se propage de la première à la dernière pièce.
• Le développement des réseaux électriques au début du 20ème siècle impose le courant alternatif dont l’énergie se transporte plus facilement que celle du courant continu (débat opposant Nicolas Tesla, adepte du courant alternatif, à Thomas Edison qui milite pour le courant continu).
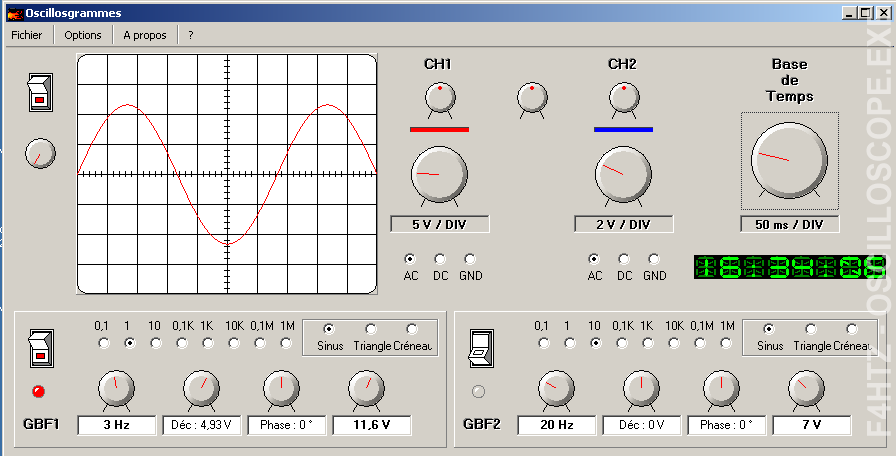
• Un oscilloscope est un instrument qui permet de visualiser sur un écran cathodique la forme d’un signal en fonction du temps.

- Le point lumineux qui parcourt l’écran représente la tension du signal et se déplace de la gauche vers la droite.
- Une sonde branchée au bout d’un câble collecte la tension à mesurer par rapport à la masse.
- Un contacteur multipositions (noté U/div) détermine la tension lue sur l’écran où sont repérées des divisions horizontales.
- Un autre contacteur (noté t/div) permet de déterminer la durée de la lecture (temps que met le point lumineux à parcourir une division de l’écran de gauche à droite).
- Les divisions verticales permettent de déterminer le temps de lecture et donc la fréquence du signal.
• Cliquez ici pour accéder au logiciel "Oscilloscope.exe".
Exemples de questions posées à l'examen
• Pulsation d'une fréquence de 1 kHz ?
- 6,28 rad/s
- 628 rad/s
- 6280 rad/s - bonne réponse
- 0,001
2 x π x F = 2 x 3,14 x 1000 = 6280 rad/s
• Fréquence d’un signal de période 500 ms ?
- 2 Hz - bonne réponse
- 2 kHz
- 0,2 Hz
- 20 Hz
500 ms = 0,5 s ; F = 1/t = 1 / 0,5 = 2 Hz
• Durée d’une période d'un signal de fréquence 2,5 MHz
- 0,4 ms
- 40 ns
- 2,5 μs
- 400 ns - bonne réponse
t = 1/ F ou t(μs) = 1 / F(MHz) = 1 / 2,5 = 0,4 μs = 400 ns (= 4 x 10-7)
Utilisez de préférence la calculette et la table de conversion pour ne pas tomber dans le piège des multiples et sous-multiples !
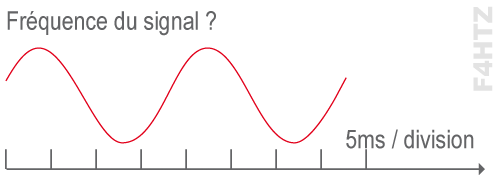
• Fréquence du signal ?
- 25 Hz
- 100 Hz
- 50 Hz
- 200 Hz - bonne réponse
la période d’observation dure : 8 x 5 ms = 40 ms, il y a 2 périodes, d’où 20 ms (ou 0,02 s) par période, d’où une fréquence de 50 Hz ( = 1 / 0,02).
• 10 V efficaces. Quelle est la tension crête ?
- 14,14 V - bonne réponse
- 7,07 V
- 28,28 V
- 20 V
Ucrête = Ueff x √2 = 10 x 1,414 = 14,14 V.
• Quelle est la valeur crête d’un signal de puissance 20 W passant dans un coaxial d’impédance de 75 Ohms ?
- 39 V
- 75 V
- 110 V
- 55 V - bonne réponse
U = √(P x R) = √(1500) ≈ 39 Volts efficaces ≈ 55 Vcrête (= 39 x 1,414 ; valeur arrondie et en supposant qu’il n’y a pas d’ondes stationnaires…)