Technique Chapitre 1 - Troisième partie
Les résistances et leurs groupements - application
01-7 Groupements Série et Parallèle
• Groupement Série
• Groupement Parallèle

Dans cette partie du cours, nous allons mettre en pratique ce qui a été vu durant les 2 cours précédents. Nous allons étudier l'approche qu'il faut adopter pour calculer la resistance équivalente ou encore, la répartition de la tension, de l'intensité et de la puissance dans un groupement de résistances en série, en parralèle ou encore, les 2 à la fois.
Comprendre la mécanique de calcul
• Beaucoup de personnes se sentent un peu dépassées au moment de rentrer dans le calcul des groupements de résistances. Pourtant c'est assez simple quand on y regarde de plus prêt.
Tout d'abord, les formules des cours précédent doivent avoir été apprises par cœur. Si vraiment vous n'êtes pas arrivé à comprendre comment fonctionnaient ces formules, alors apprenez-les bêtement sans vous poser plus de questions.
Vous allez devoir les utiliser dans ce cours. Nous allons voir comment naviguer de l'une à l'autre ou encore comment choisir la formule à utiliser en fonction de la valeur que l'on vous demande de trouver. Ce que vous allez voir ici, est bien sûr valable pour l'examen, mais vous risquez également d'en avoir besoin plus tard quand vous ferez de la radio...
Les groupements en séries
A partir de maintenant nous allons utiliser les connaissances acquises lors de cours. Si vous avez oublié une des formules, surtout n'hésitez pas à retourner sur le cours présentant les lois d'Ohm et de Joule.
Voici un groupement de deux résistances en série.
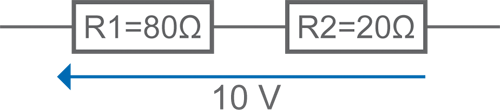
• Résistance équivalente
Pour calculer la résistance équivalente, il suffit d'additionner les valeurs des résistances.
Rt = R1 + R2 = 80 + 20 = 100 Ω
• Répartition de la tension
Voici comment il faut procéder pour connaître la répartition des tensions dans un groupement de résistances en série.
> UR1= Ut x (R1 / Rt) = 10 x (80/100) = 8 V
> UR2 = Ut x (R2 / Rt) = 10 x (20/100) = 2 V
ou par différence : UR1 + UR2 = Ut
d’où : UR2 = Ut – UR1 = 10 – 8 = 2 V
• Répartition de l’intensité
Dans ce même groupement de résistances, l'intensité se réparti comme suit :
> It = Ut / Rt = 10 / 100 = 0,1 A = 100 mA
• Répartition de la puissance
Il y a plusieurs moyens pour arriver au résultat recherché.
> Pt = Ut x It = 10 x 0,1 = 1 W
ou Pt = Rt x It² = 100 x 0,1² = 100 x 0,01 = 1 W
ou Pt=Ut² / Rt= 10² / 100 = 100 / 100 = 1 W
> PR1 = Pt x (R1 / Rt) = 1 x (80 / 100) = 0,8 W
ou PR1 = UR1 x IR1 = 8 x 0,1 = 0,8 W
> PR2 = Pt x (R2 / Rt) = 1 x (20 / 100) = 0,2 W
ou PR2 = UR2 x IR2 = 2 x 0,1 = 0,2 W
ou PR2 = UR2² / R2 = 2² / 20 = 4 / 20= 0,2 W
ou par différence : PR2 = Pt-PR1 = 1-0,8=0,2 W
Les groupements en parallèles
Bien entendu, dans un groupement en parralèle, les calculs à utiliser, ne seront pas les mêmes.

• Résistance équivalente
> Rt = Produit/Somme = (80 x 20)/(80 + 20)
= 1600/100 = 16 Ω
(formule utilisable avec 2 résistances seulement)
> ou Rt = Inverse de la somme des inverses : Rt = 1/(1/80 + 1/20) = 16 Ω
- remarque : la résistance équivalente (16Ω) est plus petite que la plus petite
des résistances du groupement (20Ω)
• Répartition de la tension
On ne peut pas faire plus simple.
> UR1 = UR2 = Ut = 10 V
• Répartition de l’intensité
> It = Ut / Rt = 10 / 16 = 0,625 A = 625 mA
> IR1 = Ut / R1 = 10 / 80 = 0,125 A
ou IR1 = It x (Rt / R1) = 0,625 x (16 / 80) = 0,125 A=125 mA
> IR2 = Ut / R2 = 10 / 20 = 0,5 A
ou IR2 = It x (Rt / R2) = 0,625 x (16 / 20) = 0,5 A = 500 mA
ou calcul par différence : IR2 = It – IR1 = 625 – 125 = 500 mA
• Répartition de la puissance
> Pt = Ut x It = 10 x 0,625 = 6,25 W
> PR1 = Pt x (Rt / R1) = 6,25 x (16 / 80) = 1,25 W
> PR2 = Pt x (Rt / R2) = 6,25 x (16 / 20) = 5 W
Les réseaux complexes
• Dans le cas d’un réseau complexe composé à la fois de résistances en Série et de résistances en Parallèle :
1- la résistance équivalente de l'ensemble le plus élémentaire sera d’abord calculée.
2- puis la résistance équivalente de cet ensemble et d’une autre résistance (ou d’un autre ensemble élémentaire) du réseau sera calculée en associant les résistances dans des ensembles de plus en plus complexes
Pour clarifier le problème, il y aura peut-être lieu de redessiner le schéma pour mettre en évidence les résistances montées en Série et celles montées en Parallèle.
• Réseau complexe n° 1
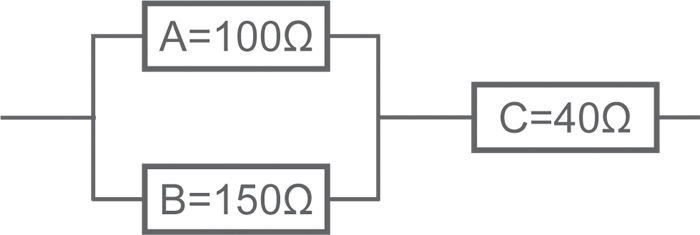
RAB = (100 x 150) / (100 + 150) = 15000/250 = 60 ; 60 + 40 = 100 Ω
ou RAB = 1 / [1/100 + 1/150] = 60 ; Rtotale= RAB+ RC= 60 + 40 = 100
• Réseau complexe n° 2
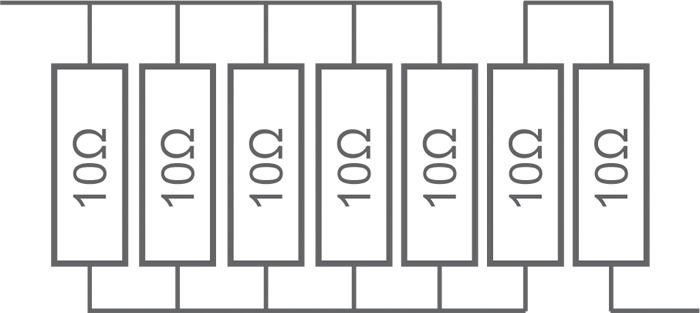
Rparallèle = 10 / 5 = 2 ; Rsérie = 10 x 2 = 20 ; Rensemble = 2 + 20 = 22 Ω
01-8 Autres exemples d’application avec des résistances
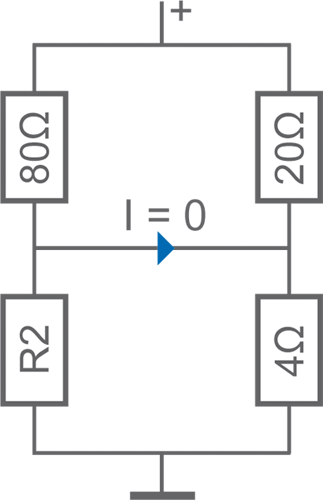 • Le pont de Wheatstone
• Le pont de Wheatstone
> Produit en croix :
R2 = (80 x 4) / 20 = 16 Ω
> plus empirique :
on voit que 4 ohms est 5 fois plus petite que 20 ohms.
Pour équilibrer le pont,
R2 sera 5 fois plus petite que 80 ohms :
R2 = 80/5 = 16
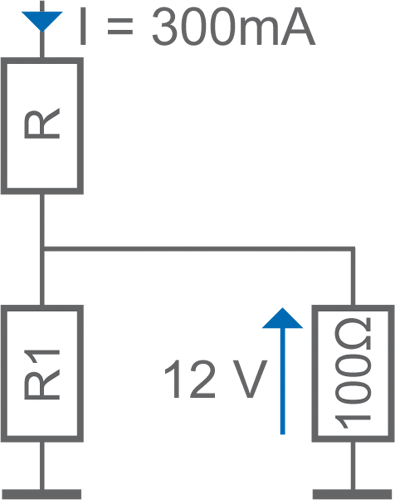 • Le pont diviseur
• Le pont diviseur
Calculer IR1 et R1
> IR2 = UR2 / R2 = 12 / 100 = 0,12 A = 120 mA
> IR1 = IR – IR2 = 300 mA – 120 mA = 180 mA
> R1 = U / I = UR2 / IR1 = 12 / 180 mA
= 12 / 0,18 = 66,7 Ω (ou 0,0667 kΩ)
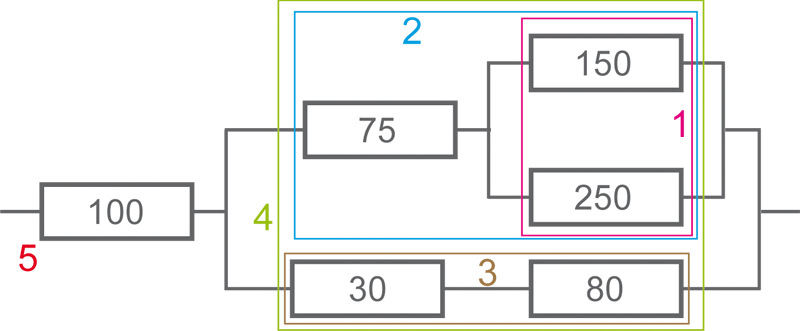 • Le réseau complexe
• Le réseau complexe
Calculer la résistance équivalente
Il faut procéder du plus élémentaire au plus complexe en 5 étapes.
- 1 : (150x250)/(150+250)=93,75
- 2 : 93,75 + 75 = 168,75
- 3 : 30 + 80 = 110
- 4 : (168,75x110)/(168,75+110)
= 66,59
- 5 : 100 + 66,59 = 167 Ω (arrondi)
Exemples de questions posées à l'examen
• Quelle est la tension totale UT ?
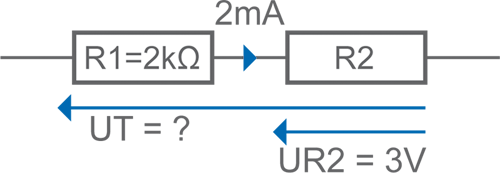
- 6 V
- 9 V
- 7 V - bonne réponse
- 2 V
UR1 = 2000 x 0,002 = 4 V ; UT = UR1 + UR2 = 4 + 3 = 7 V
• Valeur de la résistance R ?
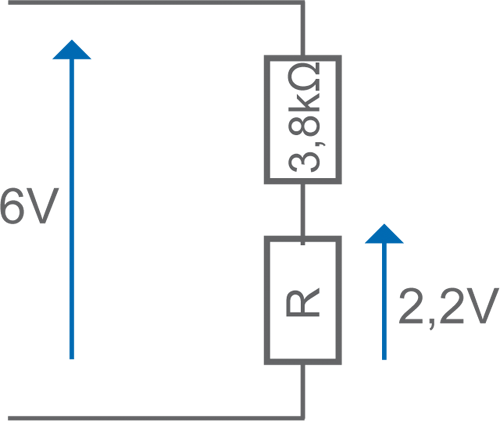
- 22 kΩ
- 2200Ω - bonne réponse
- 8,7 Ω
- 9,3 Ω
U aux bornes de 3,8 kΩ = 6 – 2,2 = 3,8V ; I dans 3,8 kΩ = U/R = 3,8/3800 = 1 mA ; R ? = U/I = 2,2/0,001 = 2200 ohms
• Résistance équivalente ?
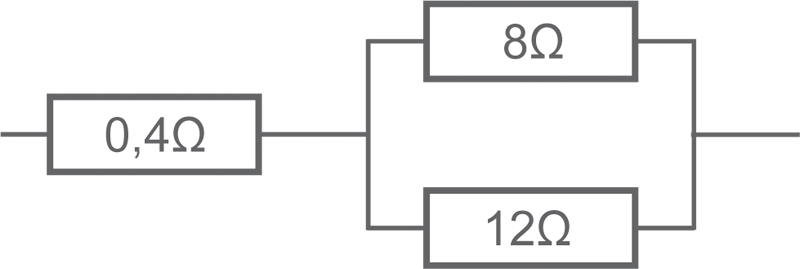
- 5,2 Ω - bonne réponse
- 1,6 Ω
- 10,4 Ω
- 0,38 Ω
produit / somme = (8 x 12) / (8 + 12) = 96 / 20 = 4,8
Résistance Totale = 4,8 + 0,4 = 5,2
• Valeur de "Rx" ?
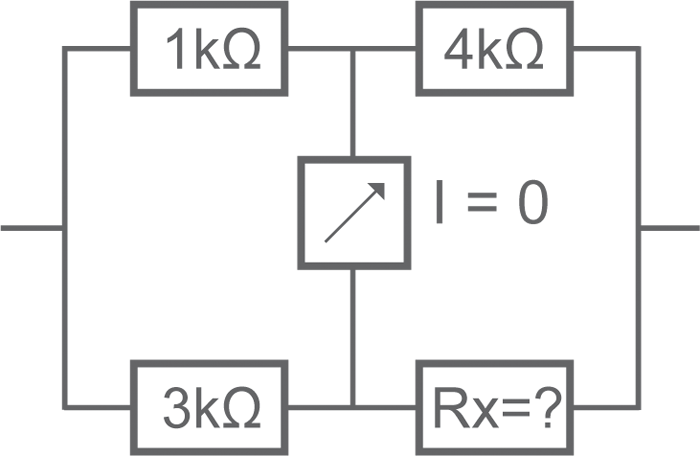
- 3 kΩ
- 4 kΩ
- 12 kΩ - bonne réponse
- 1500 Ω
Produit en croix : R = 3 x 4 / 1 = 12
• Calculer IR1
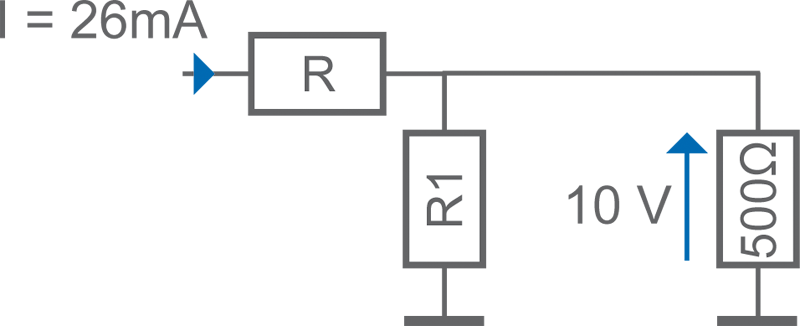
- 0,6 mA
- 6 mA - bonne réponse
- 10 mA
- 50 mA
I dans résistance 1 k = IR1k = U/R = 10/500 = 0,02 = 20 IR1 (intensité dans la résistance 1) = IT – IR1k = 26 mA – 20 mA = 6 mA
