Chapitre 1 - Deuxième Partie
Les résistances et leurs montages
1-5 Le code des couleurs
1-6 La loi des noeuds et des mailles
1-7 Groupements Série et Parallèle

Voici une partie du cours très imprtante sur laquelle vous pouvez être certain d'avoir des questions. Le code couleur des résistances vous permettra d'obtenir facilement des points. Quant aux calculs des résistances en série ou en parralèle, ils sont à connaître par cœur.
Donc, un cours très important dans la préparation de votre licence.
1-5 Le code des couleurs
• La valeur de la résistance est rarement indiquée en chiffres sur celle-ci : on utilise un code de couleurs.
• Pour coder une valeur, 3 bagues sont nécessaires :
- les deux premières bagues indiquent les deux premiers chiffres de la valeur
- la troisième bague indique le nombre de 0 de la valeur
- les bagues doivent se situer à gauche de la résistance
> Le code des couleurs est une des 10 familles de questions techniques. Il y a donc toujours 2 questions sur ce sujet.
> Une 4ème bague, décalée par rapport aux trois premières, permet de coder la tolérance des résistances (écart maximum entre la valeur indiquée et la valeur réelle). Dans les questions d’examen, cette bague est souvent représentée mais sa signification n’est pas demandée.
Il existe une expression mnémotechnique pour se souvenir du code des couleurs : l’initiale de chaque mot de la phrase correspond à l’initiale de la couleur : "Ne Mangez Rien Ou Je Vous Battrai Violemment Grand Bêta".
 Code couleurs et types de résistances
Code couleurs et types de résistances
• Les résistances du commerce ont des valeurs "normalisées". La série des valeurs des résistances à 20% de tolérance (sans 4ème bague et nommée E6) est : 10 - 15 - 22 - 33 - 47 - 68.
- Ainsi, on trouve des résistances à 20% de 1000 ohms, 1500 ohms, 2200 ohms, 3300 ohms, 4700 ohms, 6800 ohms puis on passe directement à 10.000 ohms.
• La série E12 est utilisée pour les résistances à 10% de tolérance (4ème bague de couleur Argent) dont les valeurs s’insèrent entre chaque valeur de la série E6 : 10 - 12 - 15 - 18 - 22, ...
• La série E24 suit la même logique. Les résistances de cette série ont une tolérance de 5% (4ème bague de couleur Or)
• Au delà de la série E24, pour des tolérances de 2% ou moins, les résistances sont codées avec 5 bagues : 3 bagues de chiffres significatifs suivies du multiplicateur et de la tolérance.
• Les résistances existent sous deux présentations
- en composant à fils (traditionnels)
- en composant monté en surface (CMS)
• 4 sortes de résistances sont disponibles dans le commerce
- les résistances agglomérées sont les plus anciennes et sont fabriquées à partir de poudre de carbone mélangée à un isolant et à un liant.
- Les résistances à couche de carbone : une très fine couche de carbone est déposée sur de petits barreaux isolants. La valeur est ajustée en creusant plus ou moins la couche de carbone.
- les résistances à couche métallique sont obtenues en déposant une fine couche d’un alliage résistant sur un barreau isolant.
- les résistances bobinées sont utilisées pour de faibles valeurs et sont constituées d’un fil résistant (en nickel ou cupronickel) bobiné sur un isolant. Leur utilisation en HF est une source de problèmes.
Il existe des composants dont la résistance est variable (ou ajustable), les potentiomètres et des résistances assemblées dans des circuits intégrés (DIL ou SIL) pour les applications numériques.
• Les résistances sont disponibles sous diverses puissances de dissipation maximum (fonction de la dimension du composant, de 1/8 à 2 W pour les valeurs les plus courantes). Certains composants peuvent être fixés sur un radiateur pour dissiper plus de puissance. Il faut éviter de dépasser la puissance de dissipation maximum pour garantir la valeur de la résistance et le bon fonctionnement du circuit.
• Calcul de la puissance minimum d’une résistance
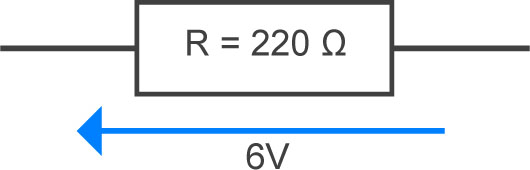 P=U2 / R = 62 / 220 = 164mW
P=U2 / R = 62 / 220 = 164mW
La première puissance supérieure proposée sera retenue(250mW par exemple ; 1/8W, soit 125mW, aurait été insuffisant).
• Il existe des composants dont la résistance est variable (ou ajustable lorsque la valeur est définie une fois pour toutes)
- Ces résistances sont montées sur un axe ou sur un curseur et peuvent être déportées (sur les faces avant par exemple) pour les réglages.
 Les potentiomètres
Les potentiomètres
- Ces composants nommés aussi potentiomètres sont montés en résistances variables (montage 1) ou en pont diviseur (montage 2).
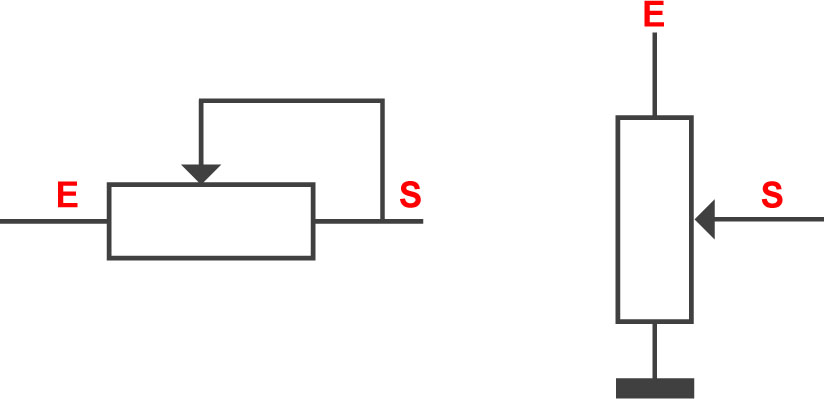 Schéma de principe
Schéma de principe
1-6 La loi des noeuds et des mailles
• La loi des noeuds et des mailles (appelée aussi lois de Kirchhoff), est très complexe. Elle n’est pas au programme de l’examen mais doit être connue dans ses grands principes pour comprendre le fonctionnement des circuits électriques et les groupements.
• Rien ne se perd, rien ne se crée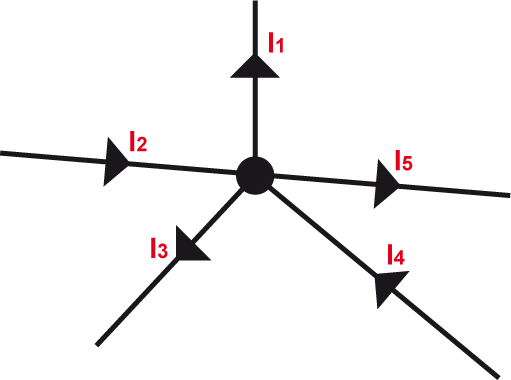
- la somme algébrique des courants passant en un noeud est nulle.
> il y a, dans un noeud (endroit où se rejoignent plusieurs fils conducteurs), autant de courant qui y entre que de courant qui en sort.
> I1 + I2 + I3 + I4 + I5 = 0
> autre présentation : I2 + I4 = I1 + I3 + I5
• Rien ne se perd, rien ne se crée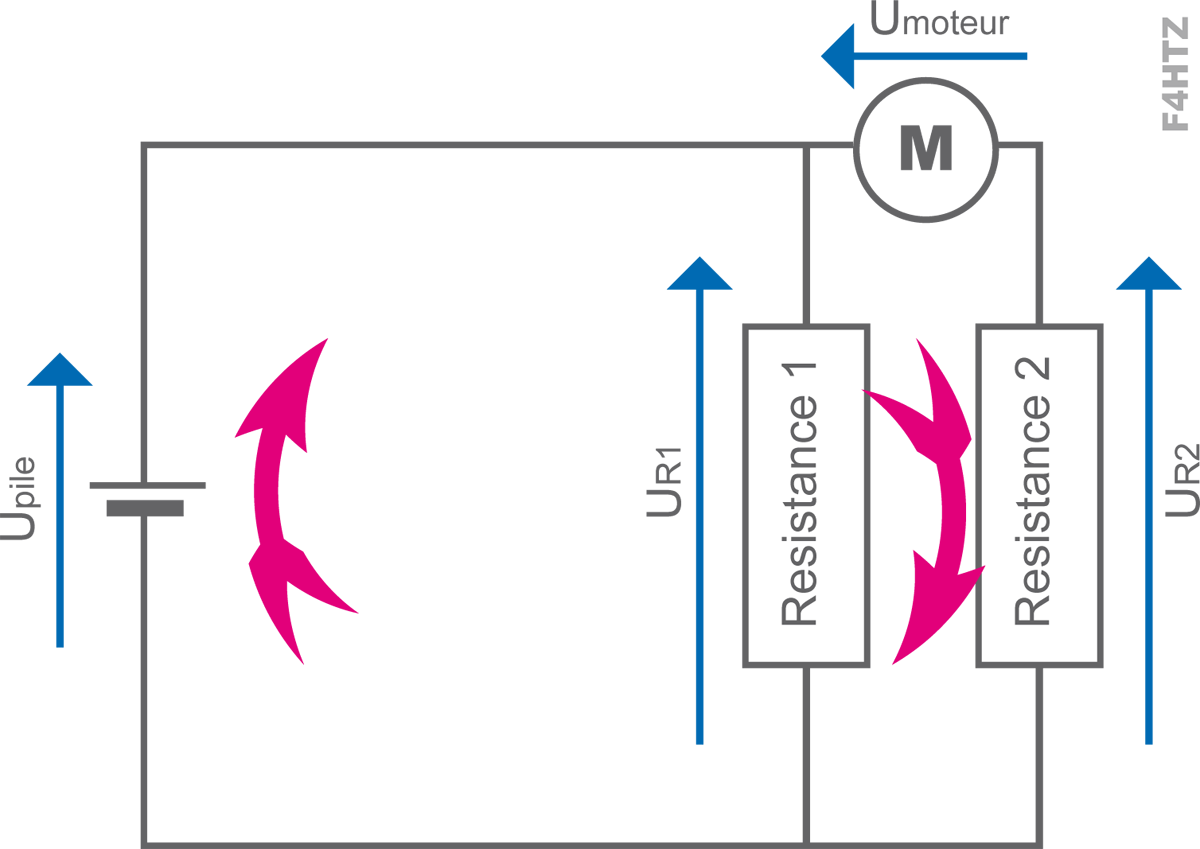
- la somme algébrique des tensions en une maille est nulle :
> quand on fait le tour de la maille (incluant la pile), la tension du générateur est absorbée par la (ou les) charge(s)
> Upile + Umoteur + UR2 = 0
> Upile + UR1 = 0
> quand on fait le tour de la maille (R1, R2 et moteur), les tensions dans chacune des branches s’annulent
> UR1 + Umoteur + UR2 = 0
> autre présentation : Upile = UR1 = Umoteur + UR2
• Le pont de Wheatstone est une application de la loi des mailles :
Le pont de Wheatstone est un instrument de mesure de résistance électrique inventé par Samuel Hunter Christie en 1833, puis amélioré et popularisé par Charles Wheatstone en 1843.
• le pont est dit "équilibré" lorsque les tensions dans chaque branche sont identiques. Ainsi, si les deux branches sont reliées en leur milieu, aucun courant ne circule (puisque I = U/R et que U=0).
1-7 Groupements Série et Parallèle
• Les résistances peuvent être groupées
- en série (les unes derrière les autres)
- en parallèle (le terme « dérivation » est aussi employé)
• En appliquant les lois d’Ohm et de Joule ainsi que la loi des noeuds et des mailles, on déduit, pour chacun des montages
- la résistance équivalente de l’ensemble
- la répartition entre chacune des résistances du groupement de :
> la tension totale présente aux bornes du circuit
> l’intensité totale parcourue dans le circuit
> la puissance dissipée totale
- enfin, nous étudierons le cas où les résistances du groupement ont des valeurs identiques.
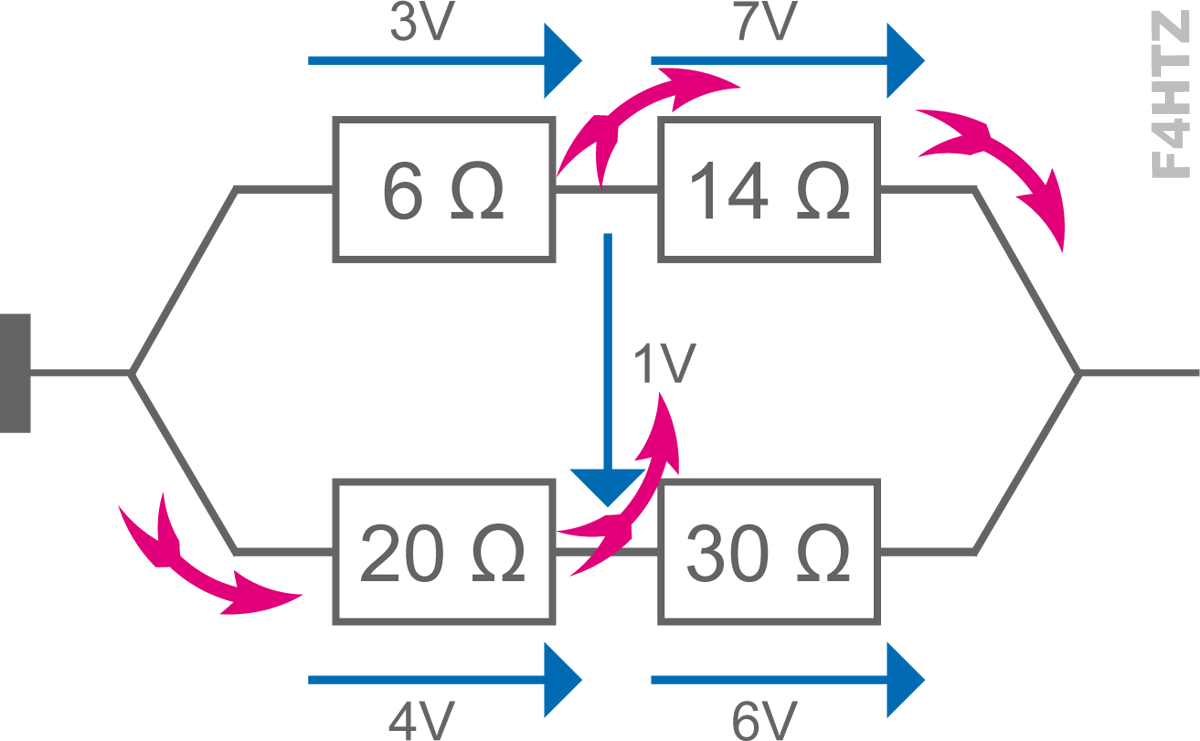
• Dans un groupement de résistances en série :
- la résistance équivalente est la somme des résistances :
> Rt = R1 + R2 +…
> est toujours supérieure à la valeur de la plus grande résistance
- la tension est répartie au prorata des résistances
> UR1 = Ut . (R1 / Rt)
> Ut = UR1 + UR2 + ... (loi des mailles)
- l’intensité est identique dans chacune des résistances
> It = IR1 = IR2 = ... (loi des noeuds)
- la puissance totale dissipée est répartie au prorata des résistances :
> PR1 = UR1 . It = Pt . (R1 / (Rt)
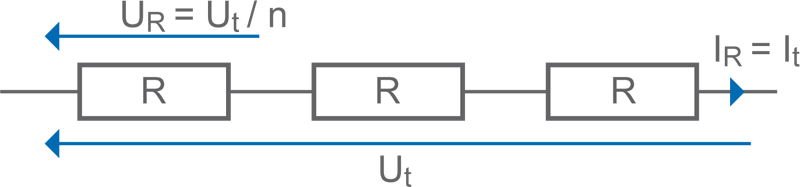
• Dans un groupement de résistances de valeurs identiques en série, on a :
- la résistance totale est proportionnelle au nombre de résistances
> Rt = R x n
- la tension est inversement proportionnelle au nombre de résistances
> UR = Ut / n
- l’intensité est identique dans chacune des résistances
> It = IR1 = IR2 = ...
- la puissance totale dissipée est répartie sur le nombre de résistances :
> PR = Pt / n
• Dans un groupement de résistances en parallèle (ou dérivation) :
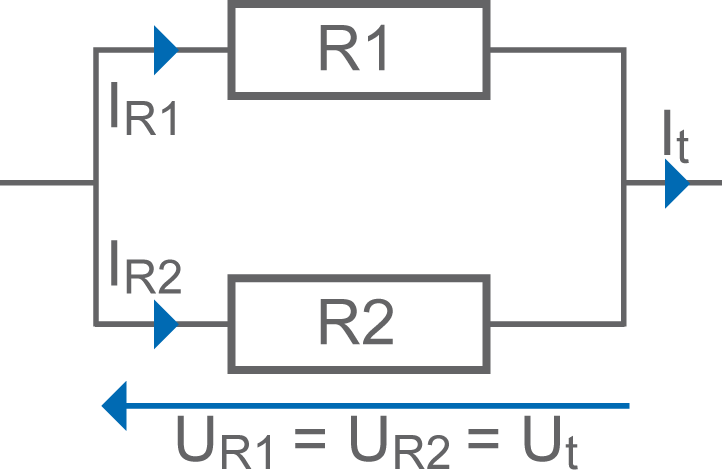
- la résistance équivalente est calculée de deux manières :
> Rt = (R1 x R2) / (R1 + R2)
. pour deux résistances uniquement
. "produit sur somme"
> Rt = 1/[(1/R1) + (1/R2) + …]
. "inverse de la somme des inverses"
. Rt est toujours inférieure à la plus petite des résistances
> la conductance équivalente est égale à la somme des conductances
. St = S1 + S2 + … (avec St = 1/ Rt )
- la tension est constante (loi des mailles)
> Ut = UR1 = UR2 = ...
- l’intensité est inversement proportionnelle aux résistances :
> IR1 = It . (Rt / R1)
> la plus faible résistance du groupement voit passer la plus forte intensité
- la puissance est répartie au prorata inverse des résistances
• Dans un groupement de résistances de valeurs identiques en parallèle :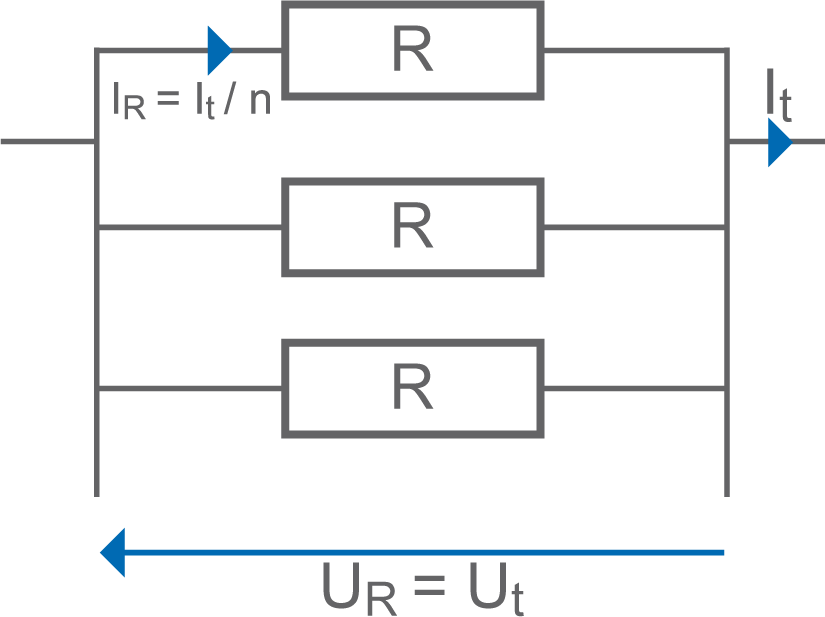
- la résistance totale est inversement proportionnelle au nombre de
résistances
> Rt = R / n
- la tension est constante
> UR = Ut
- l’intensité est inversement proportionnelle au nombre de résistances
> IR = It / n
- la puissance totale dissipée est répartie sur le nombre de résistances (comme pour les groupements en série) :
> PR = Pt / n
Un peu de pratique...
Soit un groupement de deux résistances en série alimentées par une pile et montées sur une plaque d’essai.
• déterminer la valeur des résistances à l’aide du code des couleurs, vérifier au multimètre.
> R1 = Marron - Noir - Orange - Or = 10KΩ avec une tolérance de 5%
> R2 = Bleu - Gris - Rouge - Argent = 6,8KΩ avec une tolérance de 10%

Le circuit n'est pas alimenté par la pile et le multimètre est réglé sur la mesure de la résistance (Ω).
- étape 1 : R1 mesurée = 10,20KΩ (on est dans la tolérence de 5%)
- étape 2 : R2 mesurée = 6,89KΩ (on est dans la tolérence de 10%)
- étape 3 : Rt mesurée = 17,09KΩ
• calculer la tension sur R1, vérifier au multimètre
- étape 4 : La tension mésurée de la pile est de -9,17V soit, 9,17V.
> UR1 = UPile X R1 / Rt donc UR1 = 9,17 X 10,2 / 17,09 = 5,47V

Le circuit est alimenté par la pile et le multimètre est réglé sur la mesure de la tension continue (VDC).
- étape 5 : UR1 mesurée = 5,47V
On trouve la même valeur avec le calcul qu'en mesurant avec le multimètre, ce qui est plutôt rassurant...
• vérifier la loi des mailles avec la mesure de UR2
> UR2 mesurée = 3,70V.
La loie des mailles est vérifiée :
UR1 + UR2 + UPile = 0
5,47 + 3,70 + (-9,17) = 0
Exemples de questions posées à l'examen
• Valeur de la résistance ?

0,1 Ω
1 Ω
10 Ω - bonne réponse (Marron = 1 ; Noir = 0 ; Noir = donc 10 x 100 = 10 Ω)
100 Ω
• Puissance minimum ?

1 W
2 W
5 W- bonne réponse - P = U² / R = 12 x 12 / 33 = 4,36 W. On retiendra la première puissance supérieure (5 watts). En répondant "10 W", on utilise une résistance trop grosse.
10 W
• Calcul de l’intensité I ?
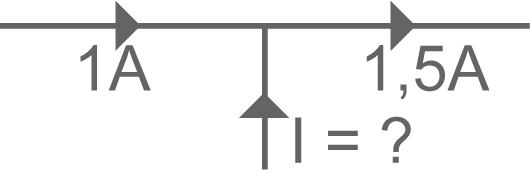
Aucun courant
0,5 A - bonne réponse
1,5 A
2,5 A
