Chapitre 1
Les bases de l’électricité
Première Partie
1-1 Les bases de l’électricité
1-2 Lois d’Ohm et de Joule
1-3 Autres unités
1-4 La résistivité

Les différentes lois qui régissent les fondements de l'électricité ont été découvertes par des chercheurs aux noms évocateurs entre la fin du 18ème siècle et le début du 19ème.
Donc en introduction, pour la petite histoire, un peu de culture générale
Alessandro Volta (1745 - 1827)
Connu pour ses travaux sur l'électricité et pour l'invention de la première pile électrique, appelée pile voltaïque. Son nom est à l'origine de l'unité de tension électrique (Volt). En 1800, un différend professionnel à propos de l’interprétation biologique de Galvani poussa Volta à inventer la pile voltaïque, une pile électrique primitive débitant un courant électrique à peu près stable. Volta savait que l'accouplement de métaux le plus efficace pour produire de l'électricité est le couple zinc-argent. Il fit d'abord l'essai de deux piles branchées en série ; chacune de ces piles était un gobelet de vin rempli de saumure, dans laquelle trempaient les électrodes ; puis il remplaça les gobelets par des lamelles de carton imbibées de saumure, interposées entre les rondelles de zinc et d'argent empilées alternativement.

Andre-marie Ampere (1775 - 1836)
Mathématicien, physicien, chimiste et philosophe français. Il a été membre de l'Académie des sciences, ainsi que professeur à l'École polytechnique et au Collège de France. Il contribue au développement des mathématiques en les introduisant en physique. Il fait d'importantes découvertes dans le domaine de l'électromagnétisme. Il en édifie les fondements théoriques et découvre les bases de l'électronique de la matière. Il est également l'inventeur de nombreux dispositifs et appareils tels que le solénoïde, le télégraphe électrique et l'électroaimant. Son nom a été donné à l'unité internationale de l'intensité du courant électrique : l'Ampère.

Charles Augustin de Coulomb (1736 - 1806)
C'est un officier, ingénieur et physicien français. Il est le premier à établir une formulation précise des lois du frottement solide, et pour l'invention du pendule de torsion, dynamomètre de précision qui lui permit de formuler la loi d'attraction entre solides électrisés. Ingénieur de formation, il est surtout physicien. Il publie sept traités sur l'électricité et le magnétisme. Ses recherches sur le travail mécanique, humain et animal, préfigurent les études de Gaspard de Prony et au-delà, préparent le taylorisme.
Coulomb est toutefois surtout connu pour les expériences historiques qu'il a réalisées à l'aide d'une balance de torsion appelée "balance de Coulomb" pour déterminer la force qui s'exerce entre deux charges électriques (loi portant son nom).

Georg Simon Ohm (1789 - 1854)
C'est un physicien allemand ayant étudié à l'université d'Erlangen.
Professeur d'université, Ohm a commencé ses travaux de recherche par une étude sur la cellule électrochimique récemment inventée par Alessandro Volta. En utilisant du matériel de sa propre invention, Ohm a découvert l'existence d'une relation de proportionnalité directe entre la différence de potentiel appliquée aux bornes d'un conducteur et le courant électrique qui le traverse, ce que l'on appelle depuis la loi d'Ohm.
Ses résultats expérimentaux lui ont permis de déterminer les relations fondamentales entre courant, tension et résistance électrique, ce qui constitue le début de l'analyse des circuits électriques.
L'ohm est devnu l'unité de mesure de la résistance électrique en son honneur.
James Watt (1736 - 1819)
Ingénieur écossais dont les améliorations sur la machine à vapeur furent une des étapes clé dans la révolution industrielle. Il a animé la Lunar Society de Birmingham. En hommage à ses recherches, le watt (symbole W), a été donné à l'Unité internationale de puissance, ou de flux énergétique (dont le flux thermique).
Watt a grandement contribué à la transformation de la machine à vapeur embryonnaire en un moyen de production d’énergie fiable et économique.
Ses améliorations sur la machine à vapeur...
La machine à vapeur conçue par James Watt a permis de passer d’une machine d’usage limité à une machine efficace aux nombreuses applications. Ce fut la source d’énergie principale de la révolution industrielle naissante, dont elle a considérablement accru la capacité de production. Avant elle, l’énergie était d'origine humaine ou animale, et, pour certaines activités (mines, travail des métaux, tissages, minoteries), hydraulique ou éolienne. Elle fut également essentielle pour les progrès qui ont suivi dans le domaine des transports, comme le bateau à vapeur et surtout le chemin de fer, avec le quasi-monopole des locomotives à vapeur jusque dans la seconde moitié du xxe siècle.

Ernst Werner Von Siemens (1816 - 1892)
C'est un inventeur et industriel allemand, magnat du génie électrique.
En 1840, dans le prolongement des idées de Jacobi sur les dépôts galvaniques de cuivre, il développe un procédé de galvanisation (notamment destiné à la dorure et l’argenterie). En 1866, il établit le principe de la dynamo électrique. cette même année, Werner Siemens et ses frères investissent dans un grand projet télégraphique, associant l'Orient à l'Europe, l'Indo-European Telegraph Company. Le nom "siemens" a été adopté comme unité du Système international pour la conductance électrique.
James Prescott Joule (1818 - 1889)
C'est un physicien anglais. Son étude sur la nature de la chaleur et sa découverte de la relation avec le travail mécanique l'ont conduit à la théorie de la conservation de l'énergie (la première loi de la thermodynamique). Il a également énoncé une relation entre le courant électrique traversant une résistance et la chaleur dissipée par celle-ci, appelée depuis le xxe siècle la loi de Joule. Enfin il a travaillé avec Lord Kelvin pour développer l'échelle absolue de température et a étudié la magnétostriction.
Dans le Système international, l'unité de l'énergie et de la quantité de chaleur porte son nom : le joule.

Il invente la loi de Joule
Et maintenant, rentrons dans le vif du sujet...
1-1 Les bases de l’électricité
L’électricité repose sur 4 grandeurs
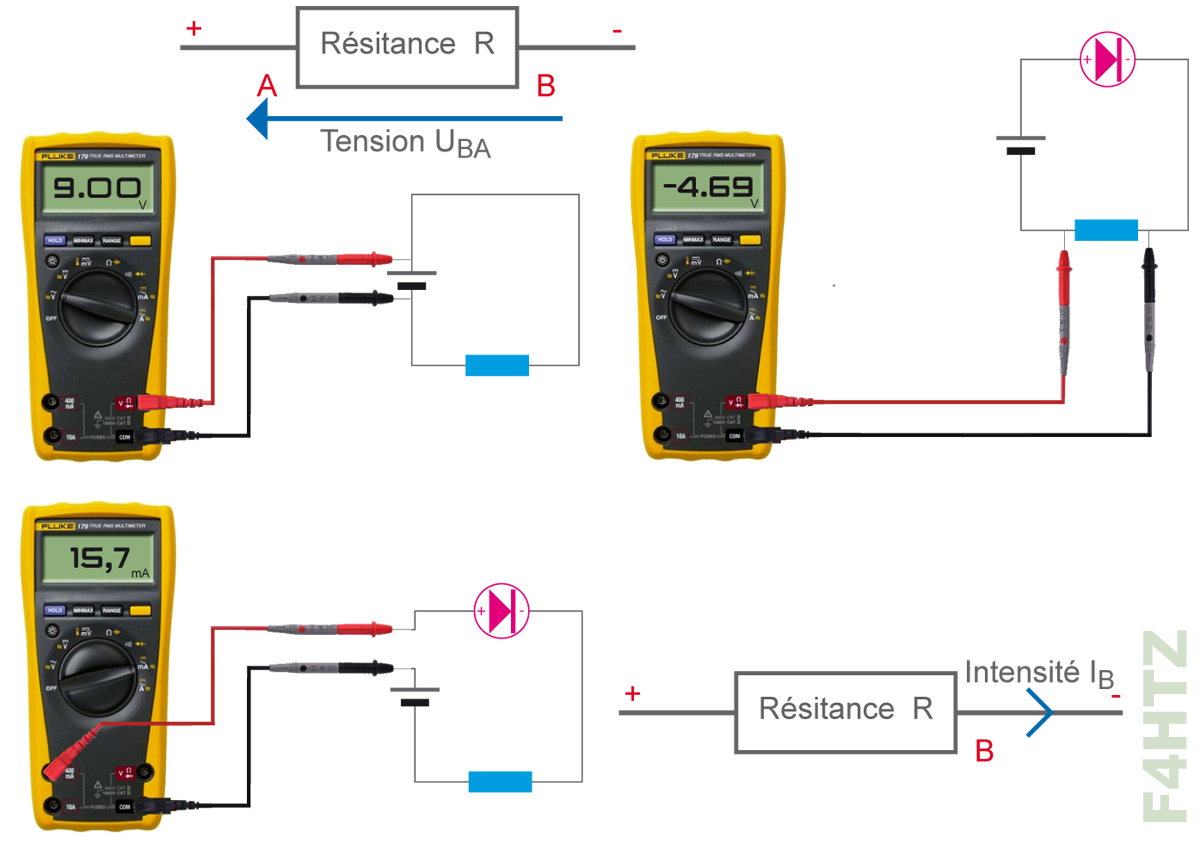
La tension
• notée U (ou E), donnée en volts (V)
• représentation
- flèche entre deux points
- tension de référence
• mesure effectuée avec un voltmètre
- force électromotrice (fém)
- différence de potentiel (ddp)
L’intensité
• notée I et donnée en ampères (A)
• représentation
- sens du courant (flèche sur le circuit)
- sens électrique et sens électronique
• mesure effectuée avec avec un ampèremètre
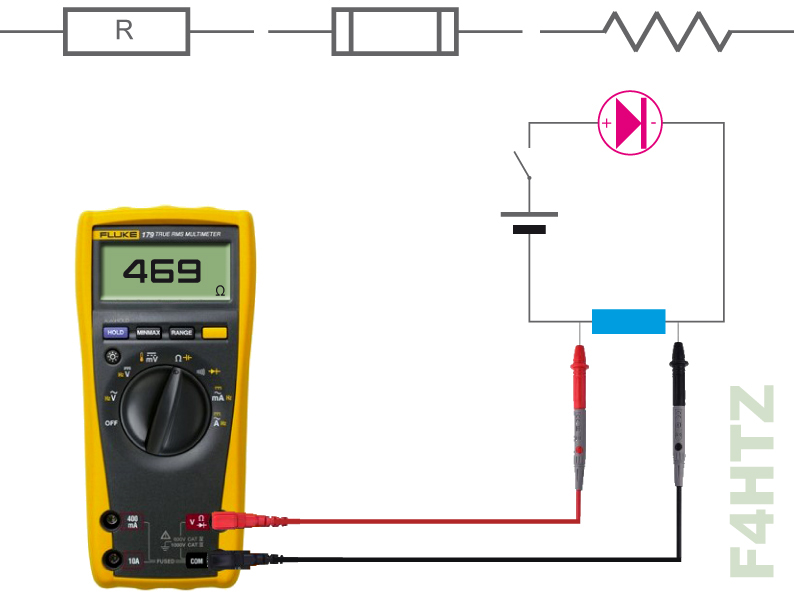
La résistance
• notée R et donnée en ohms (Ω)
• ne pas confondre le phénomène et le composant
• représentation schématique
• mesure (avec un multimètre)
• ce composant sera présenté en détail dans le prochain cours
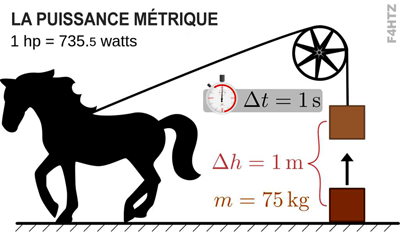
La puissance
• notée P et donnée en watts (W)
• puissance disponible
- source
• puissance consommée
- thermique (chaleur)
- électrochimique (chargement d’un accu)
- électromagnétique (champ d’une antenne)
- mécanique (moteur)
> 1 cheval-vapeur = 735,5 W = 75 kg·m·s-1
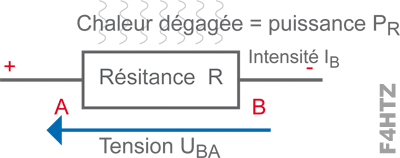
Remarque :
La puissance circulant dans une résistance correspond à une quantité de chaleur dégagée.
1-2 Lois d’Ohm et de Joule
Loi d’Ohm : U = R x I
Loi de Joule : P = U x I
• Ces deux lois sont fondamentales car elles expriment les relations entre les quatre grandeurs de base de l’électricité
• En développant ces formules (en faisant appel à l’algèbre), on obtient les relations suivantes :
R = U / I et I = U / R
U = P / I et I = P / U
• Mais aussi, en mariant les lois d’Ohm et de Joule, on obtient :
P = U x I = U x (U/R) = U² / R
P = U x I = (R x I) x I = R x I²
• De ces deux dernières formules, on peut encore obtenir les variantes suivantes :
R = U² / P U = √(PR) R = P / I² I = √(P/R)

Le tableau ci-dessus résume les 12 formules
Les quatre équations en rouge ci-dessus servent de base aux quatre triangles de calcul simplifiés qui suivent...

• Les deux premiers triangles sont ceux des lois d’Ohm et de Joule.
• Il existe aussi une autre représentation synthétique : la "roue électrique"
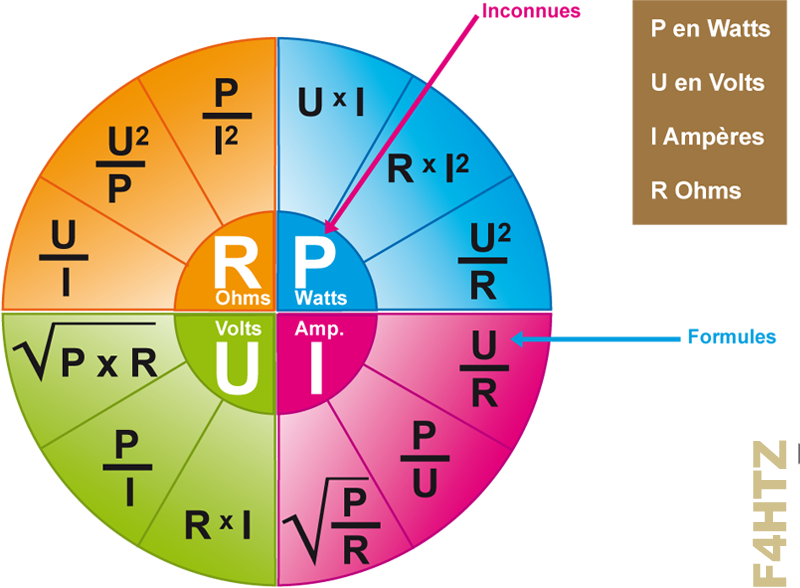
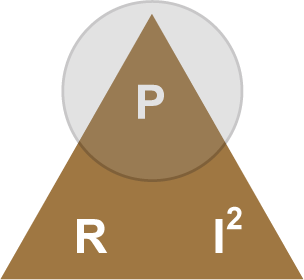
Exemples
Soit une résistance de 1500 Ω parcourue par un courant de 0.1 A.
Quelle est la tension à ses bornes ?
Quelles est la puissance dissipée ?
U = R.I = 1500 x 0,1 = 150 V ( tension aux bornes)
P = U.I = 150 x 0,1 15 W (puissance dissipée)
ou P = R.I2 = 1500 x 0,1 x 0,1 = 15 W
ou encore P = U2 / R = (150 x 150) / 1500 = 22500 / 1500 = 15 W
1-3 Autres unités
Le coulomb
• est noté C
• représente une quantité d’électricité (notée Q), c’est-à-dire un nombre d’électrons
- précisément : 6,25 1018 électrons (6 milliards de milliards)
• l’intensité est un débit et correspond au passage d’électrons par unité de temps. Un ampère est égal à un coulomb par seconde, soit la relation suivante :
- I(A) = Q(C) / t(s) ou (variante) Q(C) = I(A) . t(s)
• autre unité d’électricité : Ampère-heure (Ah) : 1 Ah = 3600 C
Le Joule
• est noté J
• représente une quantité d’énergie disponible (notée E) ou une quantité d’énergie consommée (travail et notée W)
• un watt est égal à un joule par seconde, soit la relation suivante :
- P(W) = E ou W(J)/t(s) ou E ou W(J) = P(W) . t(s)
• autre unité d’énergie : watt-heure (Wh) : 1 Wh = 3600 J

Exemples
Calculer Q en Coulombs et W en Joules pour une durée de 30 secondes.
Q(C) = I.t = (U/R).t = (10/5).30 = 2 x 30 = 60 C
W(J) = P.t = (U2/R).t = (10 X 10 / 5) x 30 = 20 x 30 = 600 J
ou W(J) = U(V).Q(C) = 10 x 60 = 600 J
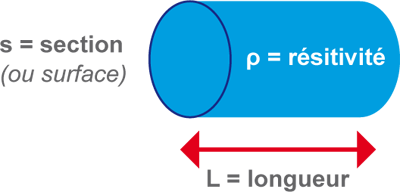
1-4 La résistivité
La résistivité est un nombre qui caractérise le pouvoir d’un matériau à résister au passage du courant électrique continu à une température définie (20°C en général).
• la résistivité est notée ρ (rhô) et se définit en Ωm.
• la résistance d'un corps dépend de sa résistivité mais aussi de ses dimensions. Si le corps est homogène, la résistance est :
- proportionnelle à la longueur
- inversement proportionnelle à la section (et non pas diamètre)
- donnée par la formule : R(Ω) = ρ(Ωm) . L(m) / s(m²)
- résistivité (ρ) de quelques matériaux à 20°C :
 résistivité des matériaux
résistivité des matériaux
- conducteur : moins de 10-5Ωm
- isolant : plus de 105Ωm

La conductivité est le pouvoir d’un matériau à laisser passer le courant électrique (inverse de la résistivité).
• notion de conductance, inverse de la résistance (en Siemens, S = 1/Ω).
Densité de courant, mesurée en A/mm²
• ordre de grandeur pour du cuivre écroui : 5A/mm²
Effet de peau : plus la fréquence du courant augmente, plus le courant se déplace en surface du conducteur, ce qui augmente sa résistance
• estimation de l’épaisseur de la peau dans un fil de cuivre :
e(μm) = 66 / √F(MHz)
9,4 mm à 50 Hz ; 0,5 mm à 20 kHz ; 66 μm à 1 MHz ;
12 μm à 30 MHz ; 5 μm à 150 MHz et 2 μm à 1 GHz
• pour limiter l’effet de peau, on pourra utiliser :
- un câble composé de plusieurs fils de petit diamètre (de préférence à un câble monobrin) car ceci augmente la section dans laquelle peut se déplacer le courant HF et donc diminue la résistance du fil
- du fil recouvert d’un matériau très conducteur (cuivre argenté) ou traité en surface de manière à ce qu’il ne s’oxyde pas (cuivre émaillé) car l’oxydation rend souvent un métal isolant.
Un peu de pratique...
Soit une résistance reliée à une pile
• Présentation d’une plaque d’essai
• A l’aide du multimètre, mesurer la tension aux bornes de la résistance et l’intensité parcourue
• En déduire la valeur de la résistance et la puissance dissipée

> L'intensité (I) mesurée est de 46 mA, soit 0,046 A.
> La tension (U) mesurée est de 9,35 V.
• La valeur de la résistance sera donc de 9,35 / 0,046 = 203,26 Ω - La résistance est décorée d'un cercle rouge puis un noir puis un marron puis un argent ce qui annonce une valeur de 200 Ω avec une précision de 5% (soit une valeur comprise entre 190 et 210 Ω), nous sommes donc tout à fait dans les attendus. Si je mesure la résistance seul à l'ohmmètre, j'obtient 202,5 Ω. Les 0,76 Ω qu'il faut rajouter pour arriver à 203,26 Ω corrrespondent simplement à l'impédance ajouter par le montage. Le compte est bon.
• La puissance dissipée sera elle de 9,35 x 0,046 = 0,4301 W soit 430 mW
Attention, en fonction de ce que vous devez mesurer, branchez vos sondes au bon endroit sur le multimètre et choisissez bien le type de musure à effectuer (La tension, le voltage, l'impédance) et attention à bien être sur le type de courant qui correspond à ce que vous mesurez (continu ou alternatif). Pour cet exercice il s'agit de courant continu, donc sélectionez "DC".
Sur la photo ci-dessus, les sondes côté multimètre sont connectées sur le "COM" pour pour la noire et sur "10A" pour la rouge. C'est normal puisqu'il s'agit d'une mesure d'intensité. Pour mesurer la tension, la sonde sur le "COM" ne bouge pas mais la sonde rouge passe sur "VΩ" (configuration qui permet de mesurer la tension ou l'impédance).
N'hésitez pas à reproduire ce petit montage chez vous. La plaque d'essai n'est pas indispensable pour un montage aussi simple mais c'était aussi une façon de vous en présenter une car nous nous en resservirons plus tard...
Exemples de questions posées à l'examen
• Quelles sont les formules exactes ?
Formule 1 : U = R + I
Formule 2 : W = P / t
Formule 3 : I = √(PxR)
Formule 4 : P = U I t
- aucune - bonne réponse
- 2 et 3
- 1, 2, 3
- 2 et 4
• Que mesure-t-on ?

- intensité - bonne réponse
- tension
- puissance
- résistance
L’appareil de mesure représenté par le rectangle avec la flèche est un ampèremètre
• Puissance dissipée par R ?
![]()
- 825 mW - bonne réponse
- 165 mW
- 6,6 W
- 8,25 W
P = R x I² = 33000 x 0,005 x 0,005 = 0,825 W = 825 mW
• Puissance dissipée dans R ?
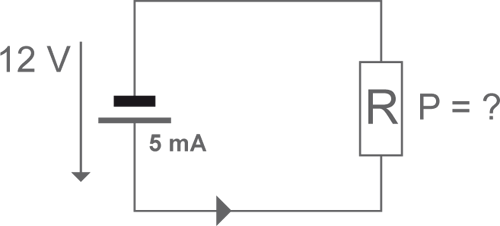
- 10 mW
- 60 mW - bonne réponse
- 100 W
- 16,7 W
P = U x I = 12 x 0,005 = 0,06 W = 60 mW
• Calculer Q
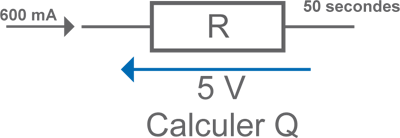
- 30 C - bonne réponse
- 250 C
- 150 C
- 417 C
Q(C) = I x t = 0,6 A x 50 s = 30 C.
la tension aux bornes de la résistance ne sert à rien dans le calcul
• Energie dissipée par R ?

- 15 kJ
- 1800 J
- 2500 J
- 9 MJ - bonne réponse
W(J) = P x t = R x I² x t = 100 Ω x 5 A x 5 A x 3600 s = 9 000 000 J = 9 MJ (mégajoules) soit 5kWh (kilowattheure)
