Introduction
Rappel de mathématiques
Première Partie
Rappels de mathématiques et d’algèbre
00-1 Transformations d’équations
• Transformations d’équations
• Puissances de 10, multiples et sous-multiples

Nous commençons ici la partie technique de ce cours de préparation au passage de la licence radioamateur.
Avant de parler purement technique radio, il est utile de faire un petit rappel mathématique. Beaucoup d'entre nous n'utilisant pas au quotidien les "maths" ont oublié tout ou partie de ce qu'ils ont appris au collège, le niveau en mathématique requis pour l'examen étant celui d'un collégiens.
Si pour vous, le collège n'est pas si loin ou si vous pensez que vos connaissances peuvent vous dispenser de suivre cette introduction au cours de technique, vous pouvez vous abstenir et commencer directement par la première partie du cours.
Transformations d’équations
• Une équation, c'est tout simplement une expression mathématique qui indique que les deux termes de chaque côté du signe "=" sont de même valeur.
• Pour résoudre une équation à une inconnue, l’inconnue (X) est isolée dans le terme de gauche en transformant les opérations :
- Addition / soustraction > changement de signe
- Multiplication / division > changement d’opérateur
- Puissance et racine carrée > changement de puissance
Voici un tableau récapitulatif de ces transformations mathématiques
 Transformation des équations
Transformation des équations
Rappel de terminologie et de présentation
• Le résultat d’une addition est une somme
• Le résultat d’une soustraction est une différence
• Le résultat d’une multiplication est un produit
- le signe (x) peut être remplacé par un point ou par rien (exemple : A x B = A . B = AB).
• Le résultat d’une division (ou fraction) est un quotien
- les deux termes sont l’un au dessus de l’autre séparés d’un trait ou sur la même ligne séparés par le signe "/ " (barre de fraction)
- le terme du haut (A) est appelé numérateur
- Le terme du bas (B) est appelé dénominateur.
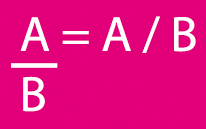
• Les opérations combinées doivent être traitées dans un ordre précis
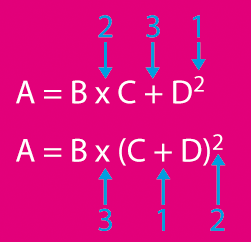
• La place des parenthèses remet en cause cet ordre
• Les expressions algébriques se simplifient en supprimant :
- les valeurs de signes opposés dans une addition : A + B + C - B = A + C
- les valeurs communes au numérateur et au dénominateur des fractions : (A x B) / (B x C) = A / C
• Soustraire un nombre négatif revient à l’additionner : 3 - (-5) = 3 + 5
• Une division par une fraction se transforme en une multiplication par l’inverse de cette fraction : 1 / (A / B) = B / A
• Si on a la relation A = B x C et que l’on cherche B ou C, on pourra utiliser la méthode du "triangle" en positionnant :
- le produit de l’équation en haut du triangle
- et les deux valeurs multipliées en bas du triangle
• Le résultat apparaît en cachant du doigt l’inconnue
- en multipliant les termes positionnés sur la même ligne
- en divisant ceux qui sont l’un sur l’autre
• Exemples
- C = A / B
- A = B x C

• Si on a la relation A / B = C / D (rapports proportionnels) et que, par exemple, D est inconnu, on détermine D par le produit en croix qui est égal :
- au produit des valeurs de la deuxième diagonale (B multiplié par C dans notre exemple)
- divisé par la valeur opposée (A dans notre exemple),
- d’où : D = B x C / A
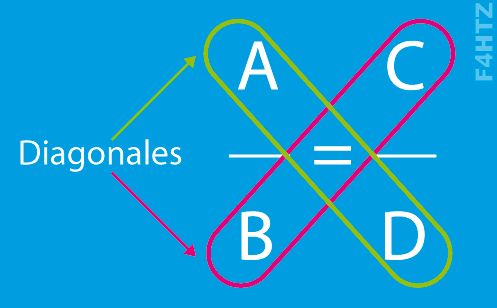
- remarque : les rapports A/C et B/D sont, eux aussi, proportionnels
00-2 Puissances de 10, multiples et sous-multiples
Voyons cela de plus prêt
• Pour faciliter la lecture des nombres qui peuvent être très grands ou très petits dans les applications radio (ou, en règle générale, en physique), les multiples et sous-multiples sont fréquemment utilisés.
• Les multiples et sous-multiples sont basés sur des puissances de 10 qui vont de 3 en 3 :
- 3, 6 et 9 pour les multiples
- -3, -6, -9 et -12 pour les sous-multiples
- chaque multiple et sous-multiple a un symbole.

• Les multiples et sous-multiples utilisés dans notre activité
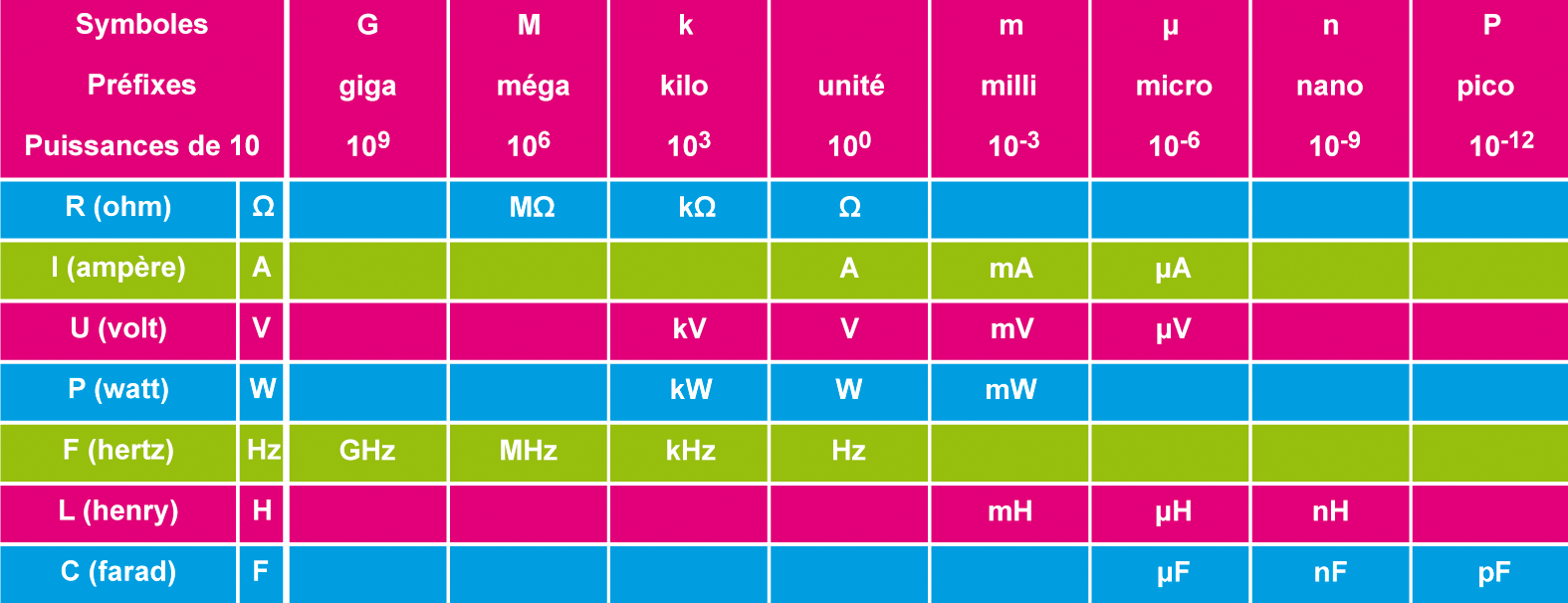
• d’autres préfixes pour les multiples et sous-multiples ont été définis :
- préfixes non multiples de 3 : hecto (symbole h, 102), déca (da, 101), déci (d, 10-1), centi (c, 10-2), myria (ma, 104).
> ces préfixes sont utilisés pour les longueurs (m), les masses (g) et les volumes (l)
- autres multiples : Téra (T, 1012), Péta (P, 1015), Exa (E, 1018), Zetta (Z, 1021), Yotta (Y, 1024), Xenna (X, 1027), Wéka (W, 1030)
- autres sous-multiples : femto (f, 10-15), atto (a, 10-18), zepto (z, 10-21), yocto (y, 10-24), xéno (x, 10-27), wéko (w, 10-30)
• Le Système International d'unités (abrégé en SI), inspiré du système métrique, est le système d'unités le plus largement employé au monde. Les formules font référence à ces unités.
- c’est un système décimal (on passe d’une unité à ses multiples ou sous-multiples à l’aide de puissances de 10) sauf pour la mesure du temps et d'angle (temps : heure, minute, seconde / angles : degré, minute, seconde).
- issu du système "MKSA", fondé sur les unités suivantes :
> Mètre, m (longueur)
> Kilogramme, kg (masse)
> Seconde, s (temps)
> Ampère, A (intensité et électricité en règle générale)
auxquelles on a ajouté un peu plus tard trois dernières unités :
> Kelvin, K (température [avec ° K =°C +273,16])
> Candela, cd (quantité de lumière)
> Mole, mol (quantité de matière)
• Pour passer d'un multiple à l'autre, déplacer la virgule de trois chiffres à chaque multiple.
• En utilisant la table de conversion ci dessous
 Table de Conversion
Table de Conversion
- positionner le nombre dans la colonne du multiple de départ avec la virgule sous le grand trait
- les cases vides à droite et à gauche seront remplies à 0.
> pour passer au multiple ou sous multiple supérieur, la virgule sera déplacée de trois crans vers la gauche (sous le premier grand trait de gauche).
> pour passer au multiple ou au sous multiple inférieur, la virgule sera déplacée de trois crans vers la droite (sous le premier grand trait de droite).
> retirer les 0 inutiles à gauche de la partie entière et à droite de la partie décimale.
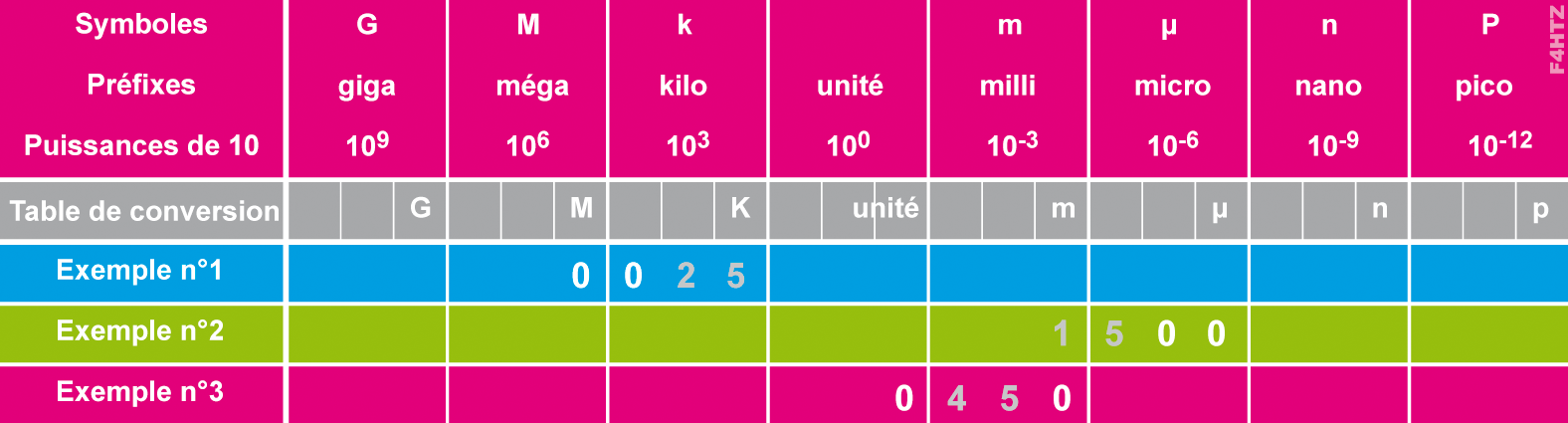
- Exemple n°1 k > M : 25 kΩ = 0.025 MΩ
- Exemple n°2 μ > m : 1500 μA = 1,5 mA
- Exemple n°3 UNITÉ > m : 0,45 V = 450 mV
Pour vous aider avant l'épreuve de l'examen, notez cette table sur votre feuille de brouillon.
• Dans les additions et les soustractions, utiliser toujours les valeurs avec les mêmes multiples ou sous-multiples.
• Dans les multiplications, les divisions et les calculs avec des puissances ou des racines carrées, faire l’opération séparément sur les nombres et les puissances de 10 :
- pour les multiplications, les puissances de 10 s'additionnent ; pour les divisions, les puissances de 10 se soustraient :
> [2.109 x 6.106]/ 3.103 = ([2 x 6]/ 3).10(9+6-3) = 4.1012
- dans les divisions, la puissance change de signe lorsqu'elle passe en dessous ou au dessus du trait de fraction :
> 1 / 2.103 = 0,5.10-3
> 1 / 5.10-6= 0,2.106
- lors de l'élévation au carré, les puissances de 10 sont doublées:
> (5.10-3)2= 52.10(-3x2)= 25.10-6
- dans les racines carrées, seules les puissances de 10 paires sont facilement utilisables car elles sont divisées par 2 :
> √(25.104) = (√ 25).10(4/2) = 5.102
Exemples de calcul
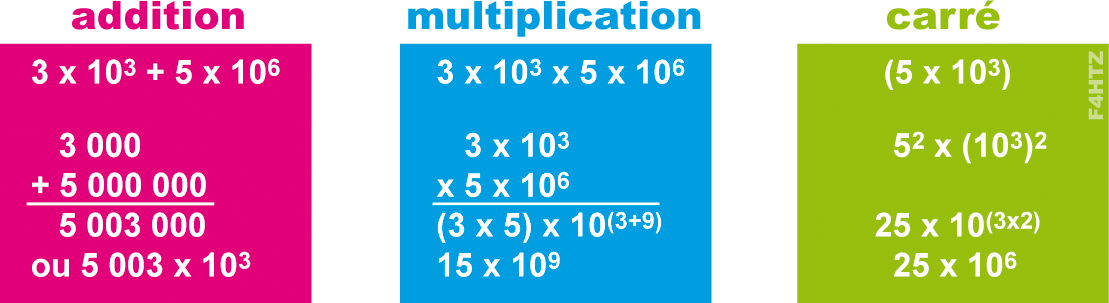
Avant d’entrer dans le détail du cours, entraînez-vous à manipuler des nombres présentés sous la forme de multiples et sous-multiples. Les pièges avec les multiples/sous-multiples sont fréquents à l’examen !
Exemples de questions posées à l'examen
Peu de questions sur ce thème mais points faciles à engranger !
• 10 microFarad = ?
- 100.000 pF
- 1000 nF
- aucune des réponses
- 1 nF
10 μF = 10.000 nF = 10.000.000 pF, donc aucune des réponses proposées

• 10 puissance -5 = ?
- 100.000
- 1/100.000 > bonne réponse : 10-5 = 1 / 105 = 1/100.000
- 0,0001
- 5
10-5 = 1/105 = 1/100.000 = 0,000 01 = 10 μ

0 -1 -2 -3 -4 -5 puissances de 10
