Chapitre 4
Deuxième partie
Circuit LC et Loi de Thomson
- Les circuits LC
- circuits bouchon et série RLC
- Filtres en pi

Nous allons étudier dans ce chapître, les différents types de filtres rencontrés chez les radioamateurs.
Les circuits LC
• Les circuits LC sont des filtres composés de bobines et de condensateurs.
• Ces filtres, s’ils sont montés comme les filtres RC (la bobine remplaçant la résistance), ont un effet de coupure.
• Seuls les circuits LC ont un effet de résonance à une fréquence lorsqu’ils sont montés en série ou en parallèle.
• Les filtres LC sont utilisés dans le domaine de la Haute Fréquence (HF) (les filtres RC ou RL sont utilisés en BF).
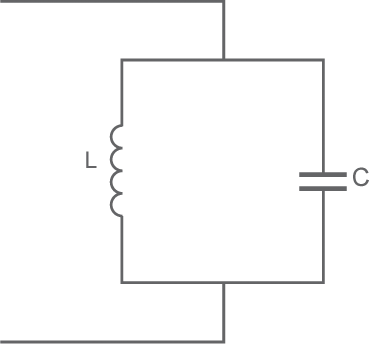 • A la résonance comme à la coupure, on a :
• A la résonance comme à la coupure, on a :
ZC = ZL => C'est la loi de Thomson
d'où :
- 1/(2πFC) = 2πFL ou, après transformation :
- F = 1 / [ 2 π √(LC) ] ou F(MHz) = 159 / (√[L(μH) . C(pF)])
William Thomson, plus connu sous le nom de Lord Kelvin, né à Belfast le 26 juin 1824 et décédé à Largs le 17 décembre 1907, 1er baron Kelvin, est un physicien britannique d'origine irlandaise reconnu pour ses travaux en thermodynamique.

Une des innovations de Kelvin est l'introduction d'un "zéro absolu" correspondant à l'absence absolue d'agitation thermique et de pression d'un gaz, dont il avait remarqué les variations liées selon un rapport linéaire. Il a laissé son nom à l'échelle de température, dite absolue, ou température "thermodynamique", mesurée en kelvins.
Ces mêmes études lui permirent d'étudier la conduction électrique des câbles sous-marins : il est promoteur de la grande construction du premier câble transatlantique. En revanche, il se heurta aux études de Maxwell sur l'éther : il se refusait à l'idée d'une propagation "transverse", sans propagation "longitudinale", dans ce milieu. Son étude de l'influence de la température sur la conduction électrique lui permit également de découvrir l'effet Thomson, ainsi que la relation entre l'effet Peltier et l'effet Seebeck, à la base de la thermoélectricité.
• Les 4 montages de base des circuits LC
- schéma des circuits passe haut et passe bas
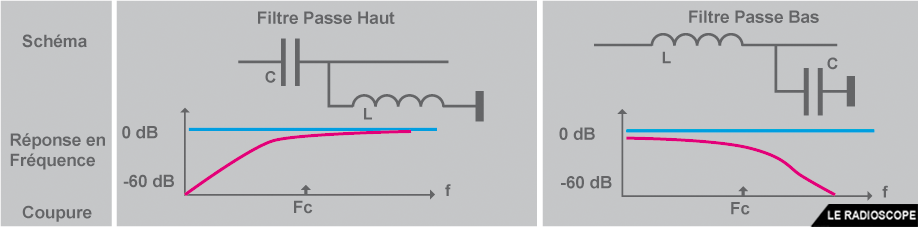
- L’atténuation d’un circuit passe bas ou passe haut est de
> 3 dB à la fréquence de coupure
> puis, à partir de cette fréquence :
.. 6 dB par octave et par éléments actifs
.. ou 20 dB par décade et par éléments actifs
.. rappel : les bobines et les condensateurs sont des éléments actifs. Donc un filtre passe bas LC simple a une atténuation de 12 dB/octave à partir de Fc.
> caractéristiques équivalentes à un filtre RC ; il y a seulement plus d’éléments actifs (au moins 2 pour un filtre LC à une cellule).

• Les 4 montages de base des circuits LC
- le circuit Série (ou circuit passe bande)
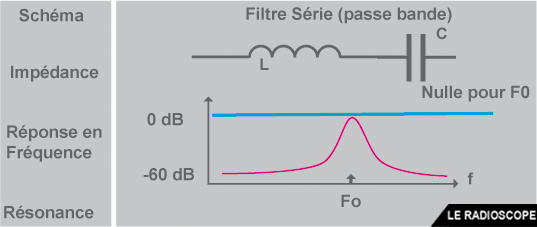
- Dans le filtre série, si le signal aux bornes du circuit est en phase avec le courant parcourant la bobine et le condensateur (effet de résonance), le signal traversera le filtre (impédance nulle).
- Remarque : une atténuation de 60 dB signifie que le signal est complètement atténué (réjection ultime).
• Les 4 montages de base des circuits LC
- le circuit Bouchon (ou circuit parallèle)
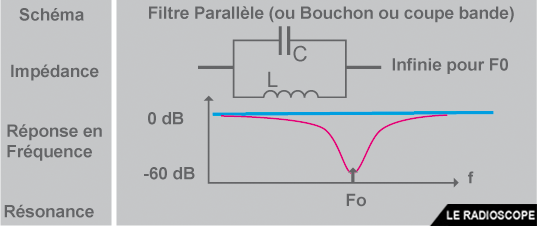
- Le filtre bouchon est un filtre utilisé pour bloquer les signaux HF d’une fréquence désirée.
- A la résonance, l’impédance très élevée (en théorie, impédance infiniment grande) du circuit empêche le courant HF de traverser ce filtre.
Exemple
• Quelle est la fréquence de résonance d'un circuit bouchon avec L = 32 μH et C = 200 pF ?
1 / (2 x [π] x [√] (32.10-6(L) x 200.10-12(C))) = 1,98944.106
(arrondi à 2 MHz)
Formule simplifiée (en retenant 1/2π = 0,16) :
160 / [√] (32 (L en μH) x 200 (C en pF)) = 2 (MHz)
(1,9875 MHz en retenant 159 au lieu de 160)
• La fréquence que donne la loi de Thomson est appelée :
- fréquence de résonance dans les circuits bouchon ou série
- fréquence de coupure dans les circuits passe bas et passe haut (comme pour les filtres RC ou RL).
• Pour baisser la fréquence de résonance (ou de coupure) d'un circuit LC, il faut :
- augmenter la valeur du condensateur,
- ou augmenter la valeur de la bobine (en particulier en introduisant un noyau magnétique à l’intérieur de l’enroulement).

• Inversement, pour augmenter la fréquence, il faut réduire la valeur du condensateur et/ou de la bobine.
- pour doubler la fréquence de résonance, la valeur du condensateur ou de la bobine sera divisée par 4 (effet de la racine carrée dans la formule de Thomson).
• Les courbes de réponse des filtres sont souvent représentées par des graphiques dont les échelles sont logarithmiques :
- l’échelle des abscisses (axe horizontal) donne les fréquences :
chaque doublement de la fréquence prend la même place.
- l’atténuation du filtre (en ordonnées, axe vertical) suit une progression logarithmique puisque les valeurs sont en dB.
• Un filtre peut être composé de plusieurs cellules LC. Dans ce cas, on repère le nombre d’éléments actifs et on applique 6 dB par octave et par élément.
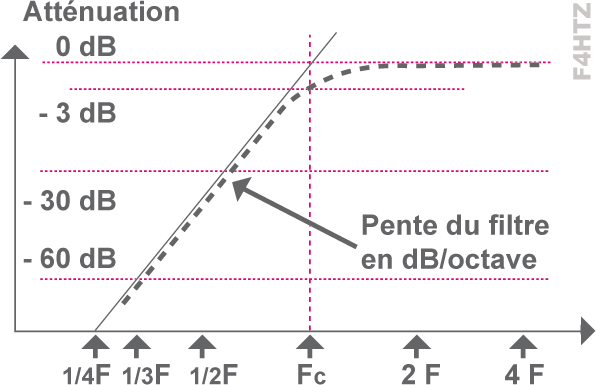
- le nombre d’éléments L et C ne détermine pas forcément les propriétés du circuit
- ci-contre : filtre passe-haut à 7 éléments actifs (42 dB/octave).
Circuits bouchon et série RLC
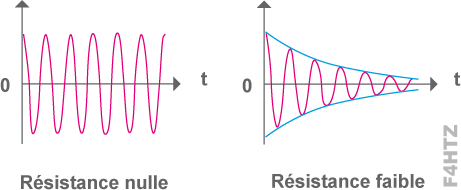
• Les circuits RLC sont des circuits LC non parfaits : le circuit est alors constitué d’un condensateur, d’une bobine et d’une résistance parasite :
- la résistance peut être en série (généralement avec la bobine représentant sa résistance à la HF, effet de peau) comme dans le circuit série (1) ou le circuit bouchon (2).
- dans le circuit (3), la résistance est montée en parallèle et représente le défaut d'isolement du condensateur.

- A cause de cette résistance parasite, l’impédance de ces 3 circuits à la résonance n’est plus nulle ou infinie.
- En revanche, la fréquence de résonance reste la même.
• Rappel : l’effet de peau fait que la résistance du fil de la bobine est plus importante que sa simple mesure à l’ohmmètre : le courant HF ne circule qu’à la périphérie du fil.
• Plus précisément, l’épaisseur "e" de la "peau" (en m) se calcule avec la formule :
e(m) = √(ρ(Ωm)/[π.μ0.μr.F(Hz)])
avec
. ρ (Rô) la résistivité du matériau,
. μo (Mû Zéro)=perméabilité du vide,
. μr (Mû r) le perméabilité du matériau où r propre au matériau du fil utilisé avec une progression similaire à la charge du condensateur (voir § 2.4).

Dans la première « peau » passe 63% du courant (63% = 1 – (1/e)) puis, dans la seconde peau de même épaisseur, passe 63% du courant restant, etc.
• voir aussi formule simplifiée au § 1.4 (valable pour du cuivre) :
e(μm) = 66 / √F(MHz)
Exemple
calculer Z à la résonance pour chaque circuit

- sans calcul, on trouve :
> Zsérie = R = 20Ω
> Zparallèle = R = 12,5 kΩ
- calcul de l’impédance à la résonance du circuit bouchon :
> Zbouchon(Ω) = L(H) / (R(Ω) x C(F))
= 25.10-6 /(20x100.10-12)
= 25.10-6 / 2.10-9
= (25/2).103 = 12,5.103
= 12,5 kΩ
• Le facteur Q définit la qualité d’un circuit RLC simple. Q est donc le facteur de qualité de notre circuit.
- Si L et C sont en série, Q est le rapport obtenu en divisant l’impédance du circuit à la résonance (Z) par la partie réactive d’un composant (XL ou XC) : Q = Z / XL = Z / XC
- Si L et C sont en parallèle, on a le rapport inverse : Q = XL / Z = XC / Z
- Rappel : à la résonance, par définition, on a toujours XL = -XC
• En appliquant ces rapports au circuit Série ou Bouchon, on obtient une formule identique : Q = √(L / C) / R
• En revanche, pour un circuit Parallèle, la formule est inversée : Q = R / [√(L / C)]
• Tableau récapitulatif de l’Impédance

• Plus Q est faible, plus la qualité du circuit est dégradée et plus l’oscillation du circuit s’amortit vite car l’énergie disponible est dissipée dans R.
- La tension aux bornes d’un circuit bouchon à la fréquence de résonance sera fonction de la puissance du signal à l’entrée du circuit et de son impédance à la résonance (d’où l’autre nom du facteur Q pour un circuit bouchon : coefficient de surtension).
- Dans un circuit série, le facteur Q est appelé coefficient de surintensité.
• Dans l’exemple du circuit bouchon, on aura :
- Q = √[L / C] / R = √[25.10-6 / 100.10-12] / 20 = 25 donc Q=25

• Rappel : même calcul pour le circuit série (Q identique si le circuit a les mêmes valeurs).
• Le facteur Q d’un circuit détermine "B" sa bande passante à –3 dB à la fréquence de résonance : B = Fo / Q
• Plus Q est élevé, plus le filtre est étroit et ses flancs sont raides et mieux les fréquences adjacentes seront rejetées.
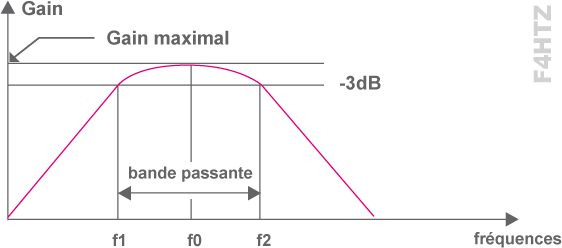
• Dans les exemples ci-dessus :
- Bbouchon = 3,18 MHz / 25 = 127 kHz
où 3,18MHz est la fréqence de résonnance de notre circuit, 25 le facteur de qualité et le résultat obtenu, 127kHz est la bande passante.
• Lorsqu’un filtre est constitué de plusieurs cellules LC
- résonant sur la même fréquence
- ou dont les fréquences de résonance sont légèrement décalées (donnant des "bosses" au sommet de la courbe),
- la courbe de réponse du filtre n’est plus définie par le facteur Q mais par deux paramètres :
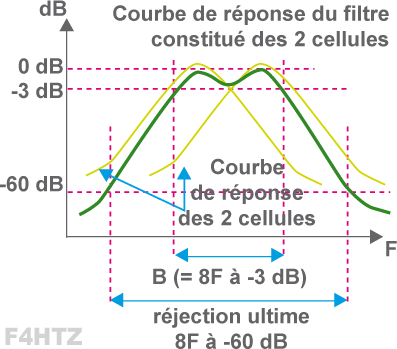
- la largeur de bande passante (définie à –3 dB)
- le taux de sélectivité égal au rapport de :
> la bande passante à -3 dB
> divisé par la bande passante à -60 dB
> le facteur de forme est le rapport inverse
Exemple
Quelle est la largeur de la bande passante à -13 dB du signal visualisé sur l’écran de l'analyseur de spectre ?
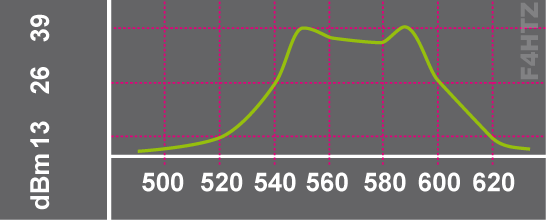
La puissance crête du signal mesure 39 dBm. La bande passante de ce signal à -13 dB est la largeur du signal dont la puissance est supérieure à 26 dBm (= 39 dBm –13 dB).
Les fréquences extrêmes du signal sont 540 et 600.
La bande passante à -13 dB du signal est de 60 (= 600 - 540)
Exemple
Quel est le taux de sélectivité ?
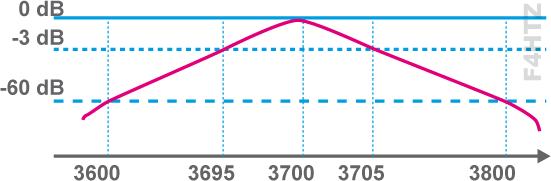
S (%) = (3705-3695)/(3800-3600) = 10 / 200 = 5%
Facteur de forme = rapport inverse = 200 / 10 = 20 (= 1/0,05)
Remarque : un circuit RLC (à une seule cellule, c’est-à-dire composé d’une résistance, d’une bobine et d’un condensateur) a toujours un facteur de forme de 1000, soit un taux de sélectivité de 0,1 %.
• L’atténuation du signal à la sortie du filtre RLC constitué d’une seule cellule suit une courbe de Gauss ("en cloche") et la bande passante du circuit pour une atténuation différente de 3 dB est donnée par la formule :
Bp = B x√(p – 1)
avec B = Fo / Q et p = rapport de puissance de la bande passante Bp (pour rappel, 60 dB = rapport de 1.000.000).
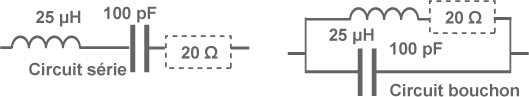
Ainsi, un circuit RLC à une seule cellule a un facteur de forme de 1000 (soit S = 0,1%) car
δF à -60 dB = √(1000000 – 1) x B ≈ 1000 x B.
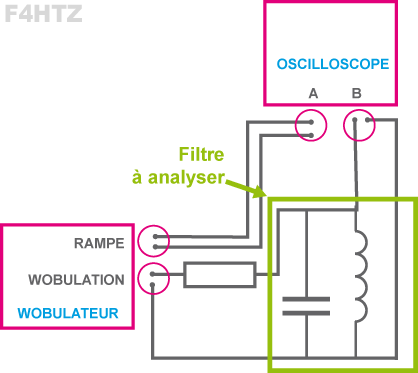
• On peut mesurer les courbes caractéristiques d’un filtre quelconque grâce à un :
- analyseur de spectre
- ou à un wobulateur (couplé avec un oscilloscope)
• Un ondemètre à absorption est un appareil de mesure de fréquence qui nécessite de la puissance pour fonctionner.
- la bobine interchangeable du circuit LC de l’ondemètre est couplée avec le signal dont on veut connaître la fréquence.
- lorsque la valeur du condensateur varie, la tension aux bornes du circuit LC lue par le voltmètre de l’appareil marque un pic très net (le "dip") indiquant que le circuit est accordé.
- la fréquence est relevée sur l’échelle de lecture du condensateur.
- si le pic n’est pas franc, il peut s’agir d’un harmonique.
- le voltmètre peut être remplacé par une lampe à incandescence dont l’éclat indique le pic de résonance.
• Un grid-dip fonctionne sur le même principe mais n’a besoin d’aucune puissance externe pour fonctionner car il possède son propre générateur HF.

- lorsque le circuit à mesurer résonne sur la fréquence de l’oscillateur, la consommation de ce dernier chute brutalement indiquant l’accord du circuit.
• Le filtre en pi est un filtre passe-bas dont l’impédance d'entrée est différente de celle de sortie grâce aux deux condensateurs variables indépendants.
- Ce filtre permet d’adapter l'impédance de l’ensemble câble + antenne avec l'impédance de sortie de l’émetteur.
- L'atténuation de ce filtre est de 12 dB par octave car les deux CV se comportent comme un seul CV (montage en série).
• Le filtre en T est un filtre passe-haut du second ordre nommé ainsi à cause de sa forme (en T) constitué d’une bobine et de deux condensateurs.
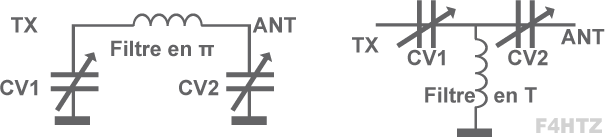
• Complément au cours
Quelques questions de l’examen portent sur les variantes des formules que nous avons développées dans ce chapitre. Voici les variantes les plus couramment utilisées :
- Pour une fréquence donnée à partir d’une des valeurs L ou C connues :
> C = 1 / 4π²F²L
ou encore : L = 1 / 4π²F²C
> formules simplifiées :
C(pF) = 25330 / F²(MHz) / L(μH)
L(μH) = 25330 / F²(MHz) / C(pF)
• Pulsation de la fréquence de résonance : ω (rad/s)= 1/√(L.C)
• Calcul de ZL et de ZC à la résonance :ZL (= ZC)= √(L / C)
• La résistance d’un circuit bouchon ou série non parfait n’est pas facilement mesurable mais se calcule.
- dans un circuit série, le facteur Q est le rapport obtenu en divisant la tension entre L et C (mesurée avec un oscilloscope) par la tension issue du générateur branché aux bornes du circuit et délivrant la fréquence de résonance.
- dans un circuit bouchon, la bande passante "B" à –3 dB du circuit est estimée à l’aide d’un grid-dip. On en déduit Q (= Fo / B)
- en connaissant L et C, on a pour les deux circuits :
R = √(L / C )/Q
- on peut aussi en déduire Z à la résonance du circuit bouchon :
Z =√(L /C) x Q
