Chapitre 4
Première partie
Décibel et circuits RC
- Le décibel (dB)
- Circuits RC

Le décibel est une unité que nous avons déjà rencontré dans la partie réglementation mais que nous allons étudier d'un peu plus près, ici.
Le décibel (dB) est une unité définie comme dix fois le logarithme décimal du rapport entre deux puissances, utilisée dans les télécommunications, l'électronique, l'acoustique, les radiocommunications... Nous étudierons également les circuits RC, CR et RL...
Le décibel (dB)
• Le décibel (dB) est une unité permettant d'exprimer un rapport entre deux unités de même nature.
Ps = puissance de sortie et Pe = puissance d'entrée.
- Schéma d’un amplificateur :
> C'est un triangle dont la base représente l'entrée et la pointe, la sortie.

La puissance appliquée à l'entrée de l'amplificateur va être multipliée par le gain en dB de celui-ci.
Alexander Graham Bel

Né le 3 mars 1847 à Édimbourg en Écosse, il décède le 2 août 1922 à Beinn Bhreagh au Canada. C'est un scientifique, un ingénieur et un inventeur scotto-canadien, naturalisé américain en 1882, qui est surtout connu pour l'invention du téléphone, pour laquelle l'antériorité d'Antonio Meucci a depuis été officiellement reconnue le 11 juin 2002 par la Chambre des représentants des États-Unis. Graham Bel déposa le premier brevet pour un téléphone en 1876. En 1888, il devint l'un des membres fondateurs de la National Geographic Society.
- rapport arithmétique > dB :
> nombre de 0 du rapport = dizaine de dB
> premier chiffre du rapport = unité de dB
- dB > rapport arithmétique :
> dizaine de dB = nombre de 0 du rapport
> unité de dB = premier chiffre du rapport
Table de conversion

Exemples
- Rapport arithmétique > dB
1) Rapport = X8 > 9dB
2) Rapport = X400 > 26dB
- Décibel (dB) > Rapport arithmétique
3) 16 dB x 40
4) 20 dB x 100
5) 33 dB x 2000.
La table de conversion simplifiée

Sur une calculatrice
• Pour passer du rapport arithmétique au décibel :
- Gain (dB) = 10 log (Ps / Pe)
- en écriture naturelle :
> 10 x [LOG] 2000 (Rapport)
= 33,013 arrondi à 33
• Pour passer des dB au rapport :
- Ps = 10 (dB / 10) x Pe
- en écriture naturelle :
> [10x] (33 (dB) / 10) = 1995,26 arrondi à 2000
> Attention, ne pas utiliser la fonction "ex", utilisée pour saisir des multiples, mais utiliser la fonction "10 puissance x" = "10x", généralement proche, sur les calculatrices, de la fonction "LOG".
• Un nombre négatif de dB inverse le rapport arithmétique et indique une atténuation et non un gain.
- –3 dB = 1 / 2
- –16 dB = 1 / (10 x 4) = 1 / 40 = 0,025
• Les décibels se calculent avec des logarithmes et possèdent donc leurs caractéristiques :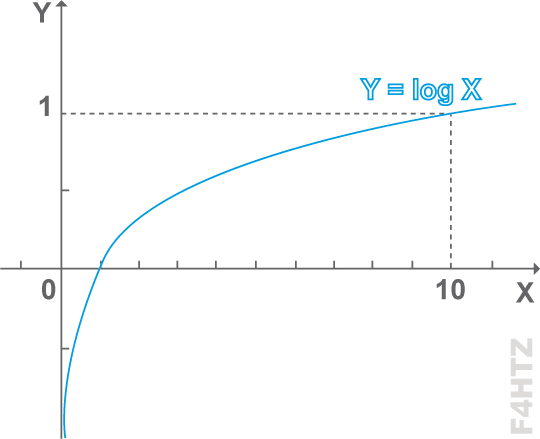
- les gains successifs (multiplication) sont transformés en addition,
- les pertes (division) sont transformées en soustraction,
- les puissances et les racines (affaiblissement linéique) sont transformées en multiplication et en division.
• La perte d’un câble est appelée l’affaiblissement linéique car elle est fonction de la longueur du câble. Cette perte est exprimée en dB/m.
Exemple
• Quel est le gain (en dB) de l’ensemble de réception représenté ci-dessous ?

• Lorsque les valeurs du rapport sont exprimées en tension, les formules deviennent :
- Gain (dB) = 20 log (Us / Ue)
- Us = 10 (dB / 20) x Ue
- le rapport des puissances est le carré du rapport des tensions (car P = U² / R). Le gain (en dB) est le double de celui calculé lorsque les valeurs sont exprimées en watts.
Exemple

> Quel est le gain (en dB) de cet amplificateur ?
= 6 dB (=3 dB x 2 ; 3 dB correspond à un rapport de puissance de 2)
> 10 μV sur une antenne de 12 dB, tension aux bornes de l’antenne ?
12 dB correspond à un rapport de tension de 4 ; Us = 4x10μV = 40μV
- même calcul si les valeurs du rapport sont exprimées en intensité (puisque P = RI²).
> Ceci n’est valable que si les impédances d’entrée et de sortie sont identiques. Si ce n’est pas le cas, le calcul se complique…
Les circuits RC
• Un harmonique est un multiple entier d’une fréquence.
- L’harmonique 3 est la fréquence de référence multipliée par 3.
• A chaque octave, la fréquence est multipliée ou divisée par 2.

- L’octave supérieure est l'harmonique 2 d'une fréquence.
- La 2ème octave est l'harmonique 4.
- La 3ème octave est l’harmonique 8 (et non pas l’harmonique 3 qui n’est pas une octave).
- L’octave inférieure (qui n’est pas un harmonique) est la fréquence de référence divisée par 2.
• A chaque décade, la fréquence est multipliée ou divisée par 10.
- La décade supérieure est l'harmonique 10 d'une fréquence.
- La 2ème décade supérieure est la fréquence multiplié par 100.
- La décade inférieure est la fréquence divisée par 10.
Exemple
Soit F = 150 kHz.
Quelle est la 5ème octave supérieure ? 2 x 2 x 2 x 2 x 2 = 32 x 150 = 4800 kHz
Quelle est la 3ème décade inférieure ? 10x10x10=1000, donc 150 kHz/1000= 150 Hz
• Un circuit RC est un filtre composé d’une résistance et d’un condensateur. Selon la place des composants, ce filtre laissera passer :
- les fréquences supérieures à la fréquence de coupure > filtre passe-haut,
- les fréquences inférieures à la fréquence de coupure > filtre passe-bas.
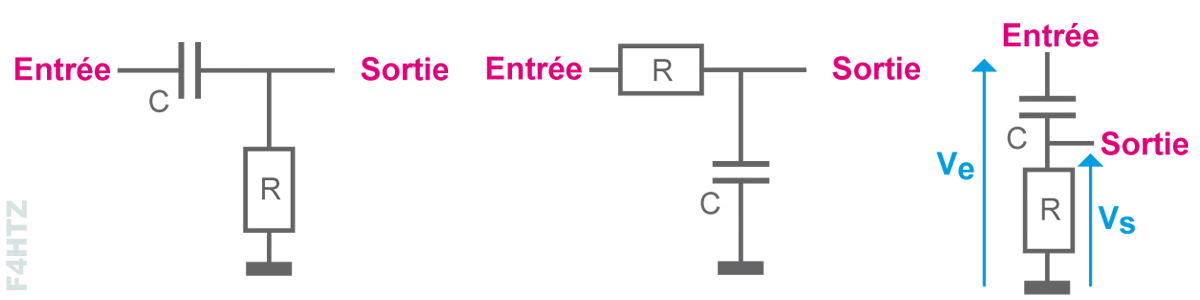
- Moyen mnémotechnique : rôle du filtre = place du condensateur.
- à la fréquence de coupure, la résistance est égale à l’impédance du condensateur, d’où :
> R(Ω) = 1 / [2π x F(Hz) x C(F)], donc :
> F(Hz) = 1 / [2π x R(Ω) x C(F)]
> Formule simplifiée de la fréquence de coupure :
F(Hz) = 159 / R(kΩ) / C(μF)
• L'atténuation de ces deux filtres est de :
- 3 dB à la fréquence de coupure (la puissance du signal à la sortie de ce filtre est divisée par 2).
- 6 dB par octave à partir de la fréquence de coupure (par octave supérieure pour un filtre passe bas et par octave inférieure pour un filtre passe haut).
- ou 20 dB par décade.
- courbe d’atténuation pour un filtre passe-haut.
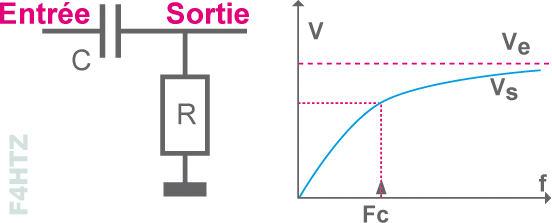
Exemple de question à l'examen
• Quelle est la fréquence de coupure de ce filtre ?
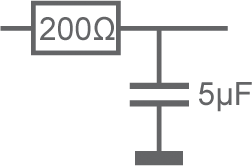
F = 1 / (2 x [π] x 200(R) x 5.10-6(C)) = 159,15.100 = 159 Hz
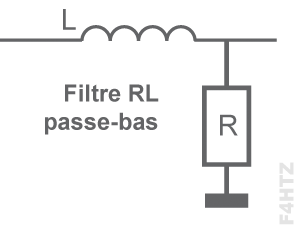
• Les circuits RL fonctionnent de la même manière que les circuits RC.
Un circuit RL passe bas aura la bobine en haut du circuit et inversement pour un filtre RL passe haut.
A la coupure, on a R = 2πFL, donc la fréquence de coupure est : F = R / (2πL).
