caractéristiques des amplificateurs opérationnels

Présentation d’un amplificateur opérationnel

• circuits intégrés :

- étapes de fabrication

- détrompage, numérotation des pattes

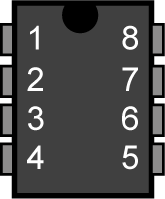
L’amplificateur opérationnel possède

• deux entrées : une normale (+) et une inverseuse (–)

• une sortie différentielle (δ).

Les amplificateurs opérationnels ont :

• une impédance d'entrée infinie (plus de 1 MΩ)

• un gain en tension (noté G) infini (gain = rapport, comme pour les transistors)

• une impédance de sortie faible (sortie connectée au + ou au -)

Caractéristiques

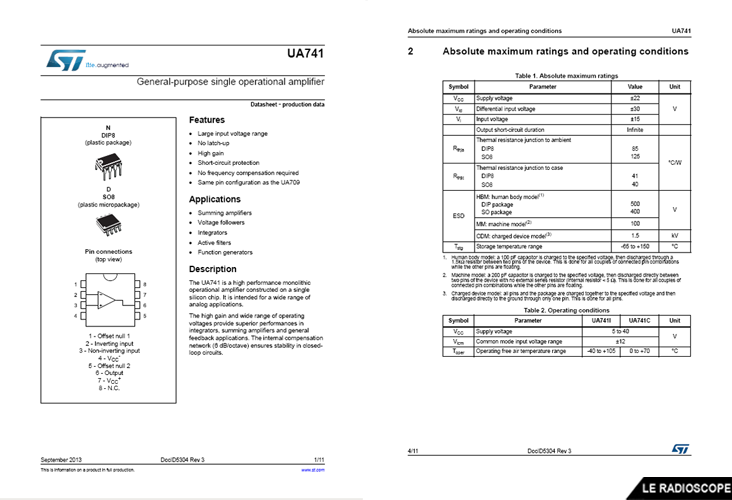
• Exemple de Datasheet sur laquelle on retrouve toutes les carractéristiques d'un μA741.

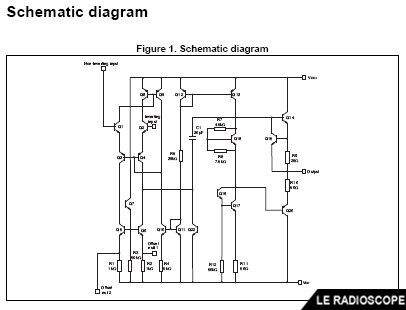
 Structure interne

• Une vue schématique extraite de la Datasheet. 

• Voici à quoi ressemble notre composant dans la réalité.

Montage fondamental des amplificateurs opérationnels

Le montage fondamental est un amplificateur inverseur de tension.

• le signal d’entrée (E) est appliqué à l’entrée inverseuse via R1

• le montage fait appel à une contre-réaction grâce à R2

• le système cherche l’équilibre pour avoir U_N = U_P

• le gain en tension à la sortie (S) est G = – (R2 / R1)

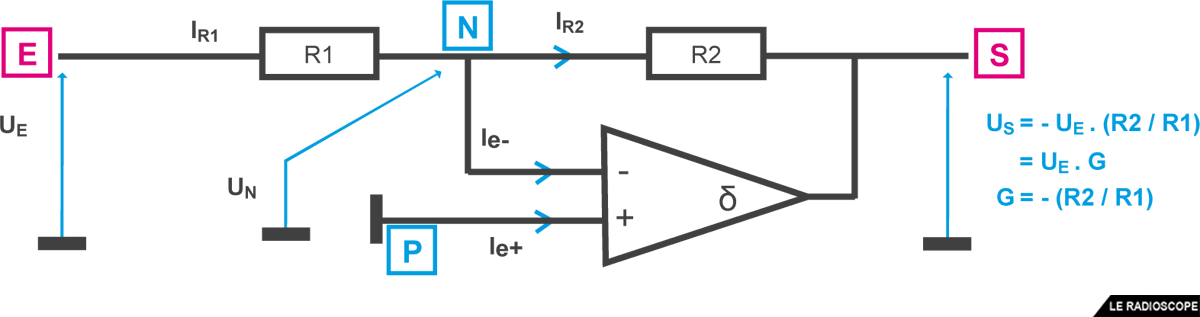
Exemple 1

Quel est le gain de ce montage ?

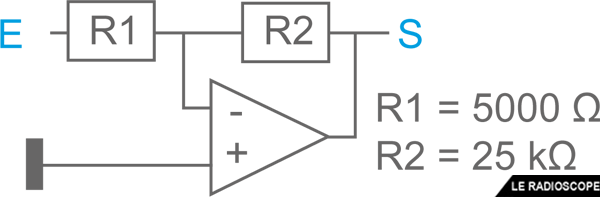
gain = - R2 / R1

= - 25kΩ / 5000 = - 25000 / 5000

= - 5

Exemple 2

Un amplificateur op monté en inverseur a un gain de –3 avec une résistance à l'entrée (R1) de 10 000 ohms. Quelle est la valeur de la résistance de contre-réaction (R2) ?

R2 = – (G x R1) = – [( –3) x 10 000] = 3 x 10 000 = 30 kΩ

Exemple 3

Quelle est la tension de sortie ?

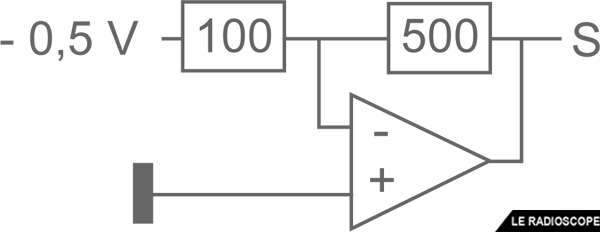
gain = - R2 / R1 = -500 / 100 = -5

Us = Ue x G = -0,5 V x -5 = 2,5 V

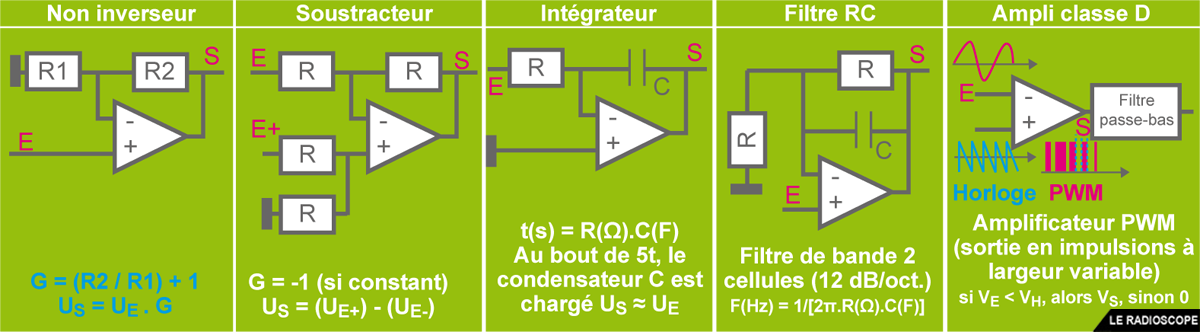
Autres montages des amplificateurs opérationnels

Seul le montage inverseur est au programme de l’examen de classe 2. Toutefois quelques questions portant sur le gain du montage non inverseur ont été recensées et il existe de nombreux autres montages.

Circuits logiques

A ce jour, aucune question recensée à l’examen mais les "circuits logiques simples" sont au programme.

• les circuits logiques sont des opérateurs binaires : ils ne connaissent que deux positions : 0 ou 1.

- Les niveaux logiques sont à 1 pour une tension proche de 5 V et à 0 pour 0 V (logique TTL).

• Les portes peuvent avoir 2 ou plusieurs entrées mais une seule sortie.

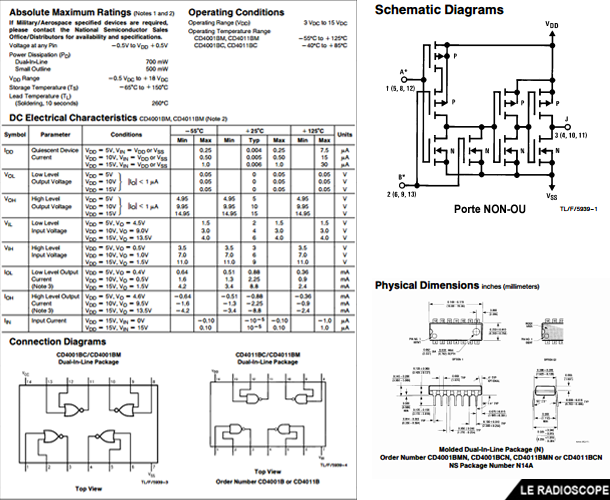
Portes logiques 4001 NOR et 4011 NAND (4 portes à 2 entrées)

• Extraits de la datasheet

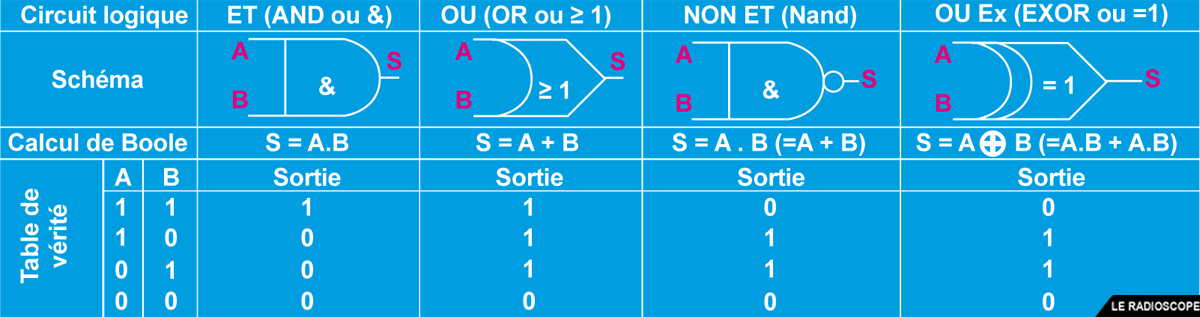
Le calcul booléen est une approche algébrique de la logique permettant de modéliser des raisonnements.

Lecture d’une table de vérité

• Exemple : porte OU (+ en calcul booléen)

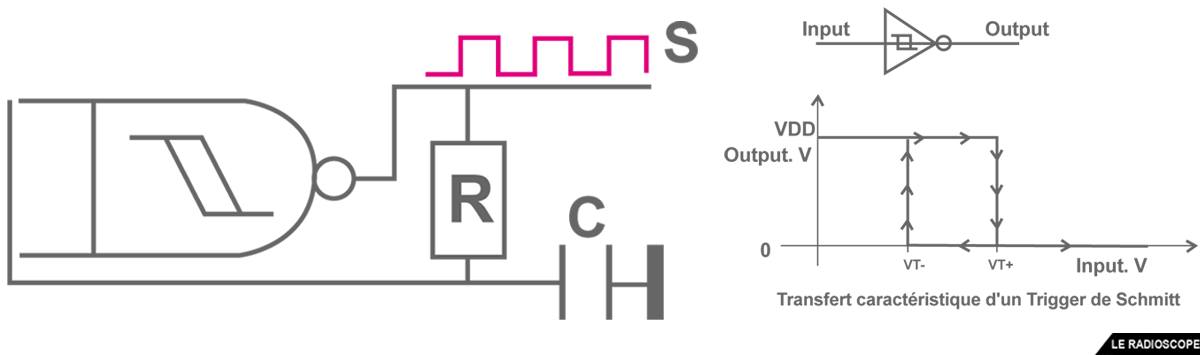
Hystérésis et trigger de Schmitt

• hystérésis (du grec usteroz (husteros) = après, plus tard) : propriété d'un système qui tend à demeurer dans un certain état quand la cause extérieure qui a produit le changement d'état a cessé.

• trigger = gâchette en anglais

• utilisation en oscillateur

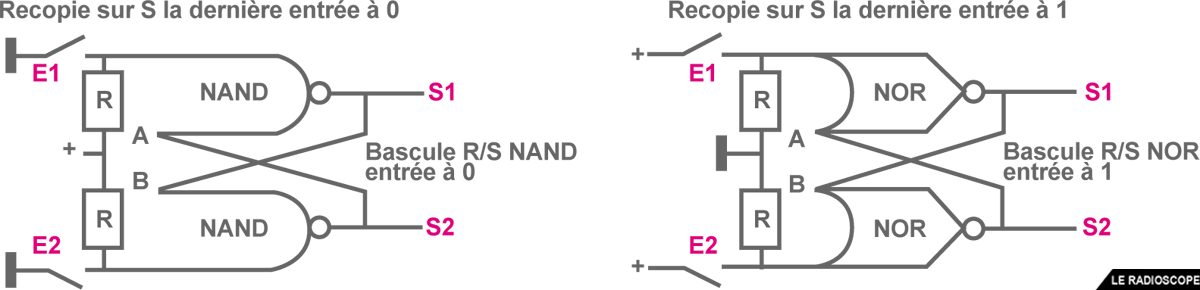
Utilisation des circuits logiques pour créer une mémoire (bascule R/S)

- R/S = Reset (=remise à Zéro) / Set (= positionner à 1)
- ces montages portent aussi le nom de "flip-flop"

• la dernière valeur présente en entrée est recopiée et conservée sur la sortie

• les sorties S1 et S2 sont complémentaires (si S1 = 0 alors S2 = 1).

• Cette technologie pour créer des "bits de mémoire" n’est plus utilisée car

- elle nécessite de nombreux composants à créer sur la puce

- elle est très gourmande en énergie

- le circuit doit toujours être alimenté pour garder les bits en mémoire

De nos jours, les mémoires de type cartes SD sont constituées de FET à grille flottante

• par rapport à un FET classique, on a ajouté un simple morceau de conducteur (créant ainsi une moitié de condensateur) appelé "grille flottante" (floating gate) parce qu’elle est isolée du reste du circuit.

• la seconde partie du condensateur est le substrat P (faiblement dopé) qui sera chargé de manière inverse de la grille flottante.

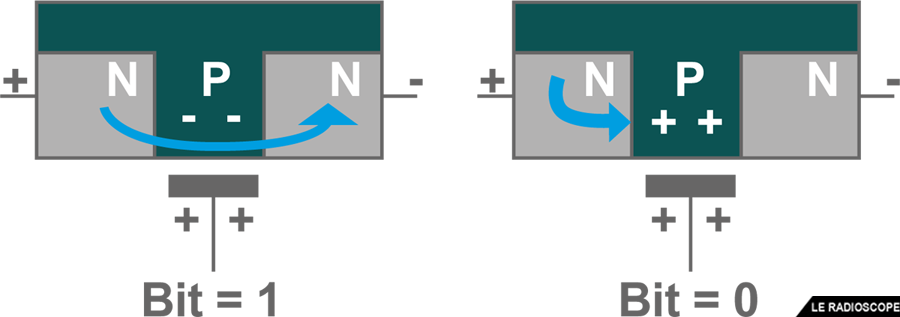
Puisque la grille flottante est isolée électriquement, son état va persister sur le long terme (effet de mémoire) même si le circuit n’est pas alimenté.

• Selon la tension présente sur la grille, le courant

- le courant ou passera (bit = 1) si la grille est chargée positivement

- le courant ne passera pas (bit = 0) si la grille est chargée négativement.

Le système binaire et le traitement numérique du signal

le système binaire repose sur les bits (BInary digiT, chiffre binaire en anglais) qui ne prennent que deux valeurs : 0 ou 1.

• un système de codage sur 8 bits formant un octet est utilisé en informatique.

• chaque octet est composé de 2 demi-octets codés en hexadécimal (base 16). Les valeurs 10 à 15, inconnues dans le système décimal, sont codées A à F selon la table ci-dessous.

Rappel : pour codifier une classe d’émission transmettant des données, on utilisera en troisième caractère la lettre D

Transmettre des données impose de vérifier que tous les bits ont été reçus correctement. Un seul bit corrompu rend les données inexploitables.

Pour être certain que tous les bits sont bien reçus, des systèmes de correction (CRC, contrôle de redondance cyclique) sont mis en place.

• dans une liaison bilatérale, après contrôle de la station réceptrice , la retransmission des données défectueuses (ARQ) par la station émettrice est demandé

• lorsque plusieurs stations reçoivent les données, le CRC ajoutera des bits de contrôle permettant la correction automatique des erreurs (FEC) par les stations réceptrices.

Un convertisseur analogique numérique (CAN ou ADC en anglais)

• prélève un échantillon (e) de la tension d’un signal à intervalles fixes (fréquence d’échantillonnage).

• la tension est transformée en nombre selon le pas de résolution (p).

La quantification est la résolution de l’échantillon (nombre de valeurs possibles du signal numérisé ou nombre de pas de résolution).

• Quantification = (U_max – U_min) / p(V)

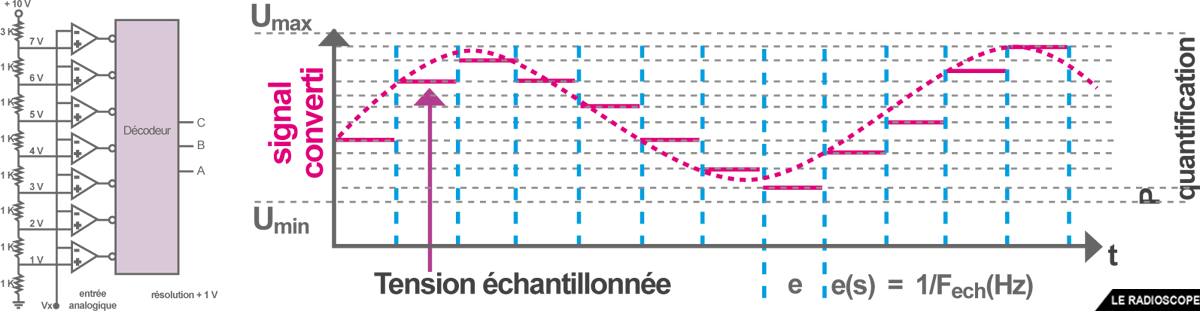
• La fréquence de Nyquist est :

- la fréquence maximum de conversion

- égale à la moitié de la fréquence d’échantillonnage F_nyquist = F_ech / 2

• Un alias est signal converti issu de fréquences supérieures à la fréquence de Nyquist.

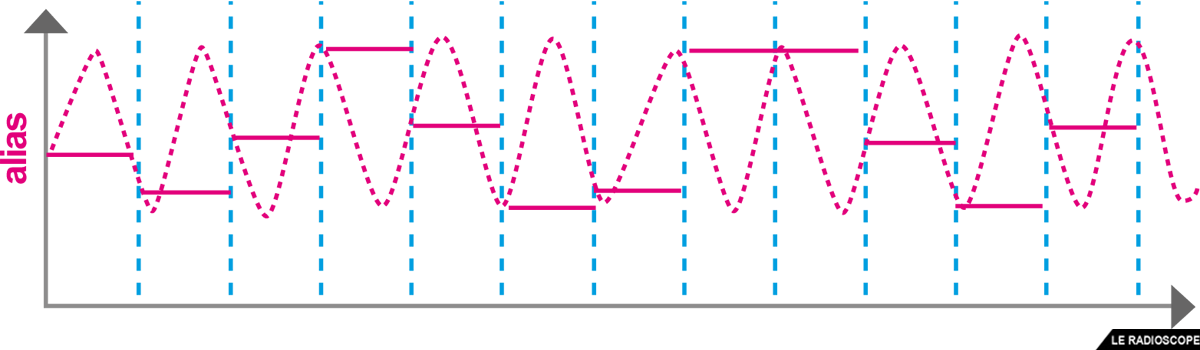
- insérer un filtre passe-bas avant le CAN pour éliminer l’alias.

Un convertisseur numérique analogique (CNA ou DAC en anglais) convertit un nombre binaire en tension.

• Il génère des "crénelages" qu’il faut éliminer à l’aide d’un filtre passe-bas (anti-harmonique) positionné après le CNA.

 • Rappel de la loi de Fourier : toutes les fonctions périodiques sont la somme de fonctions sinusoïdales de fréquences multiples de la période.

• Une Transformée Normale de Fourier (Discrete Fourier Transform, DFT) convertit un nombre fixe d'échantillons en coefficient multiplicateur des fréquences harmoniques du signal de base (convolution).

• Une Transformée Rapide de Fourier (Fast Fourier Transform FFT), utilisée dans les cartes-son, est un algorithme (programme) qui accélère le traitement en réduisant le nombre de calculs. Mais

- on perd en finesse (la définition est moins précise, risque de distorsions)

- le nombre d’échantillons à traiter doit être une puissance de 2

• Les DFT et FFT font appels aux calculs sur les nombres complexes et les matrices (bien au-delà de ce qui est demandé dans le programme de l’examen radioamateur, heureusement !)

Moins gourmands en temps de calcul que les FFT, on trouve aussi des filtres numériques

• Les filtres numériques sont réalisés à l'aide de trois éléments ou opérations de base :

• Selon leur agencement, ces trois éléments sont suffisants pour réaliser tous les filtres numériques possibles.

On distingue deux grandes familles de filtres numériques :

• les FIR (Réponse Impulsionnelle Finie)

- imitent des filtres passifs (RC, RL ou LC)

• et les IIR (Réponse Impulsionnelle Infinie)

- imitent des filtres plus complexes (filtres actifs avec contre-réaction)

Un filtre FIR (Réponse Impulsionnelle Finie) reconstitue la courbe de réponse en fonction du temps d’un filtre RC ou LC à partir de la réponse à une impulsion isolée en entrée de ce filtre

• les piles de mémoires (Z dans le schéma) servent de retardateurs.

• à chaque mémoire est affecté un coefficient multiplicateur (AN)

• chaque produit (valeurs dans Z x coefficient AN) est additionné

• la réponse du filtre FIR est finie car l’influence de l’impulsion d’entrée s’arrête lorsque tous les retardateurs ont été activés

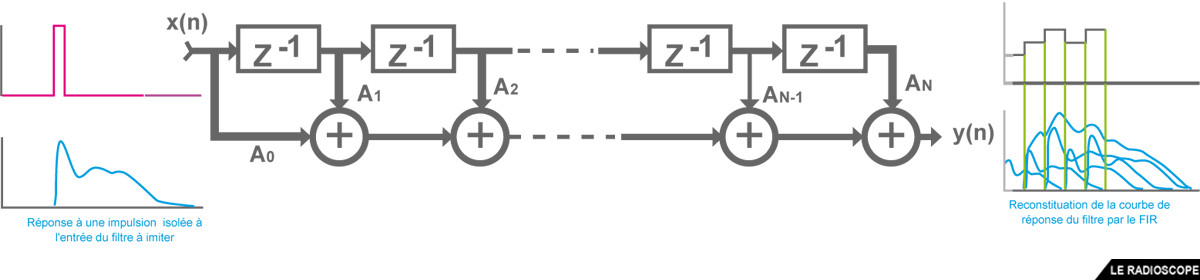
• pour un traitement unique, il y a un CAN en entrée et un CNA en sortie

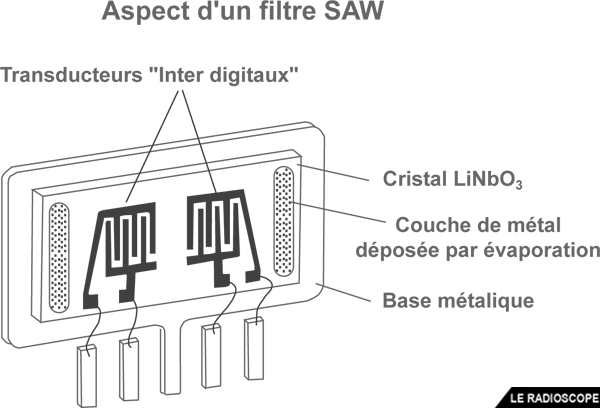
Un filtre à ondes de surface (SAW, Surface Acoustic Waves) est un filtre mécanique imitant un filtre passe-haut ou passe-bas pour une fréquence définie par le constructeur (généralement quelques dizaines de MHz).

• le signal d’entrée est converti en ondes mécaniques par un cristal piézoélectrique (voir § 7.5 sur les caractéristiques du quartz).

• les ondes sont affaiblies et retardées lors de leur propagation dans le cristal avec les mêmes coefficients et retards qu’un filtre FIR puis sont recombinées en sortie pour générer le signal filtré.

• Mais le filtre FIR a des limites dans la reconstitution d’un filtre : un filtre actif avec contre-réaction ne peut pas être imité.

• On a alors recours au filtre IIR (Réponse Impulsionnelle Infinie), plus complexe à mettre en oeuvre, dont la rétroaction vient corriger sur chaque retardateur le résultat du FIR à partir duquel il est construit.

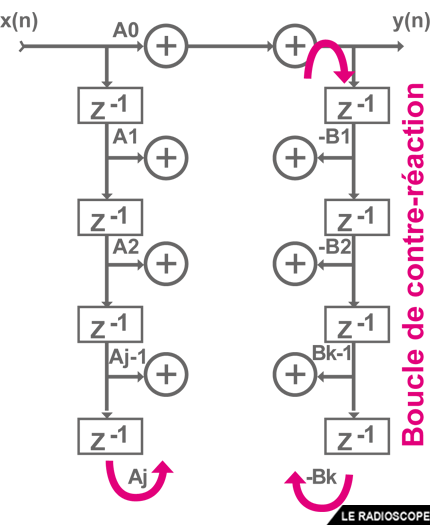
• La réponse du filtre IIR est infinie car, en théorie, la rétroaction perdure indéfiniment avec le risque d’auto-osciller

- plusieurs types de montages sont disponibles

- il faut adapter les coefficients multiplicateurs en fonction du montage utilisé et du filtre à imiter

- comme pour les FIR, on trouve un CAN en entrée (sauf si le signal est déjà numérisé) et un CNA en sortie