Chapitre 10
Lignes de transmission et adaptations ...
- Lignes de transmissions (feeders)
- Impédance et coefficient de vélocité
- Adaptation, désadaptation et ondes stationnaires
- lignes d'adaptation et symétriseurs

Lignes de transmissions (feeders)
La ligne de transmission est utilisée pour transférer l'énergie
Trop souvent négligée, la ligne de transmission est pourtant un des élements constitutif de la chaîne de transmission qu'il nous faut prendre en compte. Si non, quel serait l'intérêt de construire une antenne à fort gain pour tout perdre via la ligne de transmission ?
• de l'émetteur vers l'antenne
• ou de l'antenne vers le récepteur.
La ligne de transmission peut être
• asymétrique (câble coaxial)

• symétrique (ligne bifilaire)

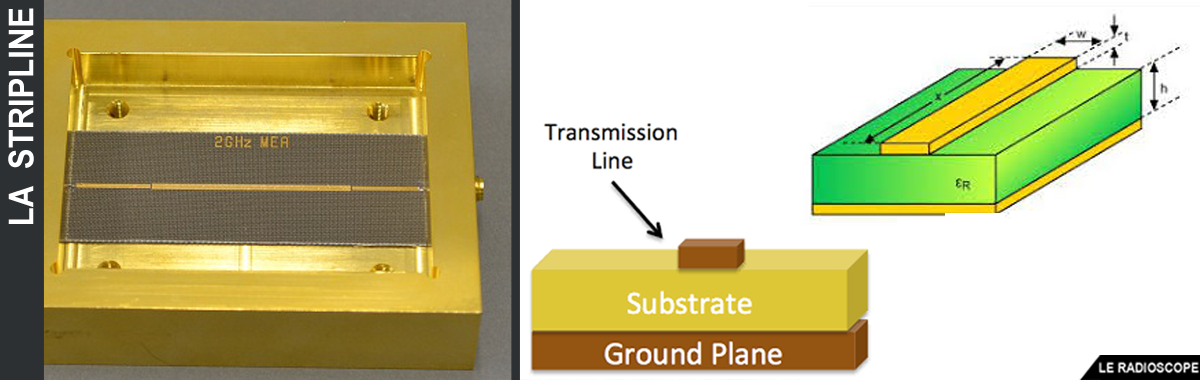
• strip line (gravée sur un circuit imprimé)
Une ligne de transmission est équivalente à un circuit constitué
• d’une bobine,
• d’un condensateur
- le rapport √(L/C) fournit l'impédance caractéristique (en Ω).
• et de deux résistances (une en série, l’autre en parallèle)
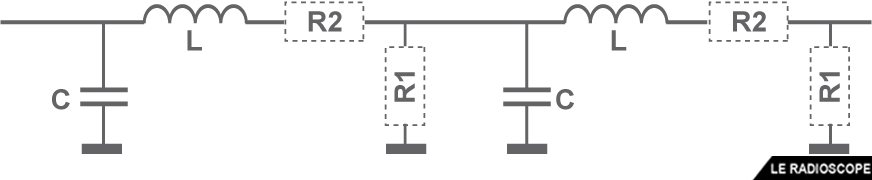
La valeur des résistances détermine la qualité de la ligne
• en série (la plus faible possible) : liée à l’effet de peau qui augmente avec la fréquence
• en parallèle (la plus forte possible) : fuites d’isolement et conductance linéique due aux défauts du diélectrique utilisé lorsque la fréquence transférée est supérieure à 1 GHz
La qualité de la ligne se définit par sa perte (en dB/m).
• la perte est donnée par le constructeur (souvent en dB /100 m).
• la perte augmente avec la fréquence du signal transféré et est moindre dans une ligne bifilaire que dans un câble coaxial.
• la perte en fonction de la longueur de la ligne, appelée aussi affaiblissement linéique, se calcule avec les décibels
- cette perte n'a aucun rapport avec l’impédance de la ligne.
Si les courants dans les deux fils (ou âme et tresse) sont conjugués (égaux et de valeurs contraires),
• la ligne de transmission fonctionne en mode différentiel
• et la ligne ne rayonne pas.
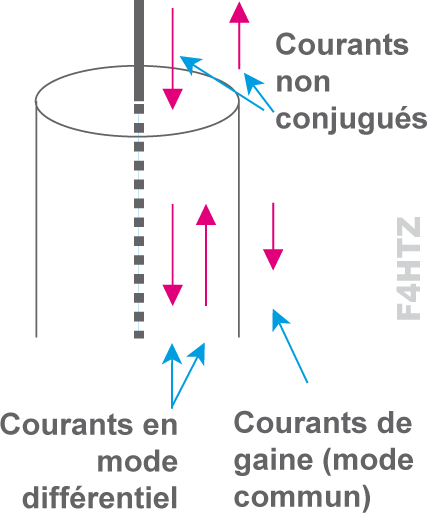
Lorsque les courants ne sont plus conjugués, signe d’une désadaptation,
• la ligne fonctionne en mode commun
• la ligne rayonne comme une antenne long fil à cause du courant de gaine.
• On peut insérer un "choke balun" pour limiter (étouffer) le courant de gaine.
Impédance et coefficient de vélocité
Si un signal est appliqué à l’entrée de la ligne, un signal de même impédance se retrouvera à la sortie (en négligeant les pertes) si et seulement si la ligne est bouclée sur une résistance (ou une charge non réactive) égale à l’impédance caractéristique de la ligne calculée selon la formule :
Zligne(Ω) = √(ZL.ZC) = √(ωL/ωC) = √[L(H/m)/C(F/m)]
(formule issue des lois de Maxwell)
Exemple
Quelle est l'impédance du câble suivant ?
• L = 0,5 μH/mètre
• C = 200 pF/mètre
Réponse : Z = √(0,5.10-6/ 200.10-12) = √(2500) = 50 Ω
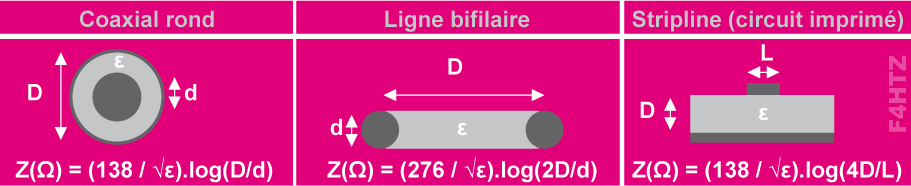
Autre manière de calculer l’impédance d’une ligne :
• à partir des dimensions des conducteurs (D et d ou L)
• et du diélectrique employé (ε) puisque Zligne = √[L /C]
Le guide d’onde n’est pas une ligne de transmission : les ondes sont transférées par réflexion sur les parois conductrices d’un tube entre deux transitions (sortes d’antennes qui font l’adaptation câble-guide).
• le guide d’onde a des pertes moindres qu’un câble coaxial mais ne peut transférer que des fréquences dont la demi-longueur d’onde est inférieure à sa plus grande dimension.
• exemple : largeur maxi tube (L) = 3 cm -> λ < 6 cm -> F > 5 GHz

La fibre optique est un guide d’onde transférant de la lumière à l’intérieur d’un fil de verre ou de plastique translucide. Mais ce n’est plus de la radio !
On rappelle que le vide a
• une perméabilité μo de 4π.10-7 H/m (soit 1,26 μH/m) et
• une permittivité εo de 1/36π.10-09 F/m (soit 8,84 pF/m)
la formule de Maxwell définit l’impédance du milieu de propagation:
Zmilieu = √[ZL x ZC] = √[2πFL x 1/(2πFC)] = √[L /C]
le vide a une impédance de √[L/C] = √[1/36π.109 x 4π.10-7]
= 120π = 377 Ω (et non pas ∞)
• Ne pas confondre impédance du milieu de propagation et résistance d’isolement.
De plus, la loi de Maxwell définit la vitesse de propagation des ondes :
L.C.c² = 1
d’où c = 1/ √(L x C) = 1 / √[1/36π.109 x 4π.10-7] = 3.108 m/s
• la vitesse de propagation des ondes est toujours arrondie à 300.000 km/s
• les permittivité et perméabilité relatives de l’air sec sont très proches de celles du vide (μr = 1,00068 et εr = 1,0014) si bien que les impédances de l’air sec et du vide et les vitesses de propagation dans ces deux milieux sont égales.
Dans un fil ou dans un câble, la vitesse de propagation des ondes est plus faible que dans l'air ou dans le vide.
La vélocité est la vitesse du courant dans le câble (en % de la vitesse dans l'air ou le vide) et dépend uniquement du diélectrique utilisé (ε). Puisque c = 1/ √(L x C), on a :
v(%) = 1/√ε
les principaux diélectriques utilisés et leur vélocité :
• 1,0 pour l’air sec ou le vide 100%
• 1,1 à 1,2 pour l’air avec écarteurs 95% à 91%
• 1,5 pour le PE expansé semi-aéré 80%
• 2,1 pour le téflon 69%
• 2,3 pour le PE 66%
• 3,7 pour la bakélite 52%
• 4,5 pour la fibre de verre 47%
Adaptation, désadaptation et ondes stationnaires
Le transfert de puissance entre un générateur de courant alternatif et une charge est maximal lorsque l’impédance du générateur est
• égale à celle de la charge
• de signe contraire, si il y a une réactance.
• les impédances sont alors conjuguées.
Dans les exemples ci-dessous, on cherche laquelle des 3 résistances (R1, R2 ou R3) dissipe le plus de puissance ?
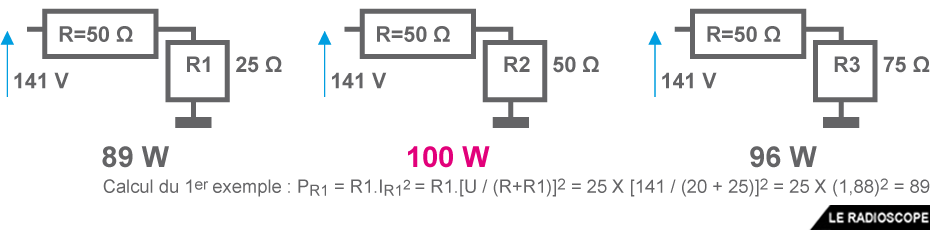
La désadaptation des impédances entraîne qu’une partie de la puissance émise, la puissance réfléchie, retourne au générateur.
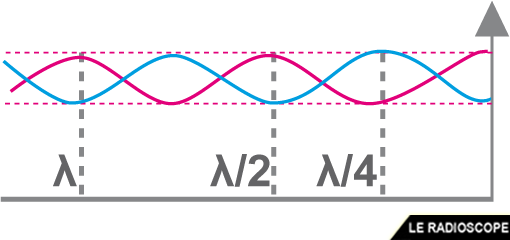 • Deux courants en sens inverse se superposent dans la ligne et, à certains endroits, les tensions et les intensités s’additionnent (ventres) et à d’autres, elles se soustraient (noeuds).
• Deux courants en sens inverse se superposent dans la ligne et, à certains endroits, les tensions et les intensités s’additionnent (ventres) et à d’autres, elles se soustraient (noeuds).
- si Zcharge < Zcâble, il y aura un noeud de tension
- la tension (en bleu) et l’intensité (en rouge) sont déphasées de 180°
• Les endroits où se situent ces maxima et ces minima sont fixes (d’où le nom d’ondes stationnaires) par rapport à la charge et dépendent de la fréquence.
• Ils sont distants les uns des autres d’un quart d’onde. Le phénomène se répète donc toutes les demi-ondes.
- Attention à la vélocité du câble dans le calcul des distances.
Le TOS et le ROS sont deux mesures de la désadaptation et sont liées par la loi d’Ohm :
• par le coefficient de réflexion, nommé ρ (rhô) et égal au rapport du courant réfléchi divisé par le courant émis (en V ou en A).
ρ = UR / UE = (Umaxi - Umini)/(Umaxi + Umini)
ρ = IR / IE = (Imaxi - Imini)/(Imaxi + Imini)
- le TOS (Taux d’Ondes Stationnaires) est égal à 100 fois ρ.
TOS (%) = ρ x 100
- si les valeurs mesurées sont en Watts, la puissance réfléchie est égale à la puissance émise multipliée par le carré du coefficient de réflexion
ρ = √(PR / PE ) ou Préfléchie = Pémise x ρ²
• par le rapport des valeurs maxi/mini (en Ohms, Volts ou Ampères) appelé ROS (rapport d’ondes stationnaires).
ROS (rapport / 1) = Zmaxi(Ω) / Zmini(Ω)
ou ROS (rapport / 1) = Umaxi/Umini = Imaxi/Imini
Exemple
Quel est le TOS ?
• UE = 100 V et UR = 4 V
Réponse : 4/100 = 0,04 = 4%
Quel est le ROS ?
• Z coax = 50 Ω et Z doublet λ/2 (= 75 Ω)
Réponse : 75/50 = 1,5/1
• Z coax = 50 Ω et Z antenne verticale l/4 (= 36 Ω)
Réponse : 50/36 = 1,3888 = 1,4/1
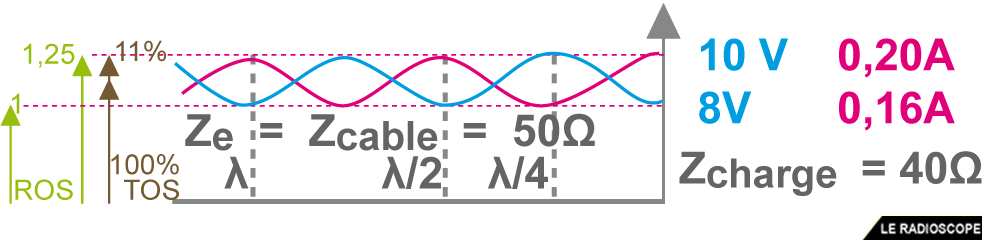
Dans le schéma ci-dessous, quels sont le ROS et le TOS ?
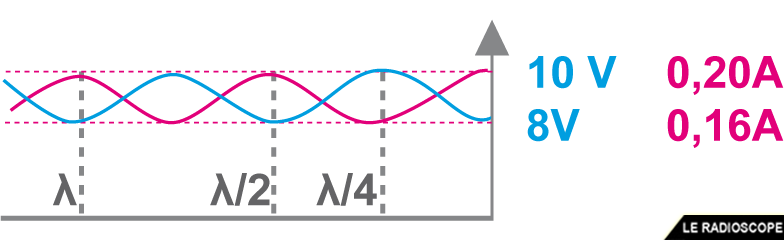
• ROS = Vmaxi / Vmini = 10 / 8
(ou Imaxi / Imini = 0,2 / 0,16) = 1,25/1
• ρ = [(10 – 8) / (10 + 8)]
(ou [(0,2 – 0,16) / (0,2 + 0,16)]) = 0,111
soit TOS = 11%
Pour la transformation du ROS en ρ (ou en TOS) et inversement, les formules suivantes sont utilisées :
ROS = (1+ρ)/(1–ρ)
ρ = (ROS–1) /(ROS+1)
Peu de questions sur l’utilisation de ces deux formules à l’examen

Complétons le schéma de l’exemple précédent :
• impédance de l’onde émise : 9V / 0,18A = 50Ω
• impédance de l’onde réfléchie : 1V / 0,02A = 50Ω
• le générateur délivre une tension de 9 V et la tension réfléchie est de 1 V (ou 0,18A et 0,02A réfléchi). (TOS = 11%)
• la désadaptation résulte ici d’un rapport d’impédance de 50 / 40 (ROS = 1,25/1).
• le taux de puissance réfléchie est ρ² = 1,23 % (=1/9²)
• valeurs maxi et mini de U (en bleu) et I (en rouge) :
- Zcâble = Umaxi/Imaxi = Umini/Imini = 10 / 0,2 = 8 / 0,16 = 50Ω ;
- Zcharge = 8 / 0,2 = 40Ω
- Pémise = U²/R = 9²/50 = 1,62 W = Pcharge en régime établi
- Pcharge début régime transitoire = U.I = 8 x 0,2 = 1,6 W = Pémise x (1-ρ²)
Des complications lorsque l’impédance est réactive
• l’intensité et la tension ne sont plus déphasées de 180°
Régime transitoire :
• lorsque l’onde réfléchie atteint le générateur, elle est renvoyée vers la charge (en se superposant à l’onde émise par le générateur)
• où elle sera une nouvelle fois partiellement absorbée
• jusqu’à ce que le système se stabilise
• tenir compte des pertes dues à l’affaiblissement linéique
Régime établi :
• lorsque le système est stabilisé,
• toute la puissance du générateur est absorbée par la charge
• dans la ligne, il y a plus d’énergie (celle émise + celle réfléchie + les allers-retours jusqu’à la stabilisation du système) mais les rapports ROS/TOS restent identiques.
Le fait d’insérer une boîte de couplage entre la ligne et l’émetteur protège l’amplificateur final mais ne solutionne pas les problèmes liés à la désadaptation (pertes supplémentaires liées au ROS, mode commun, …).

Une boîte de couplage peut être constituée d’un filtre passe-bas en pi permettant d’accorder l’impédance de la ligne et de sa charge avec celle de l’amplificateur.
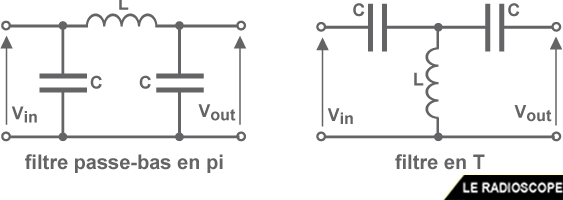
Le filtre en T est aussi utilisé pour adapter les impédances mais celuici ne fait pas office de filtre passe-bas.
Lignes d'adaptation et symétriseurs
Si les impédances de la charge et de la ligne ne sont pas égales, il y a des ondes stationnaires dans la ligne de transmission et l’impédance ramenée à l’entrée peut avoir des composantes réactives (inductives ou capacitives).
Toutefois, pour certaines longueurs de ligne, les composantes réactives s’annulent :
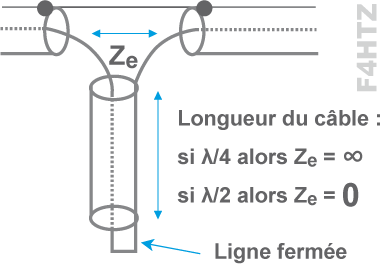
• à chaque demi-onde, on a
Ze = Zs
• à chaque nombre impair de quart d’onde, on a
ZC² = Ze x Zs
ou ZC = √(Ze . Zs)
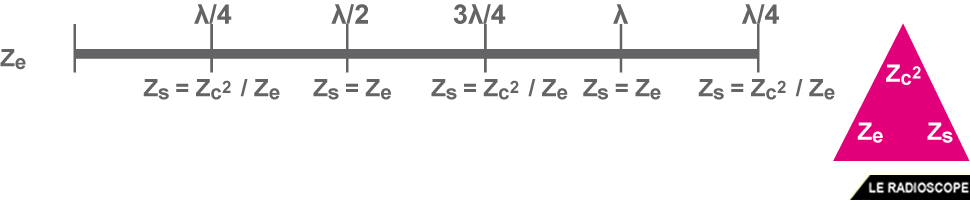
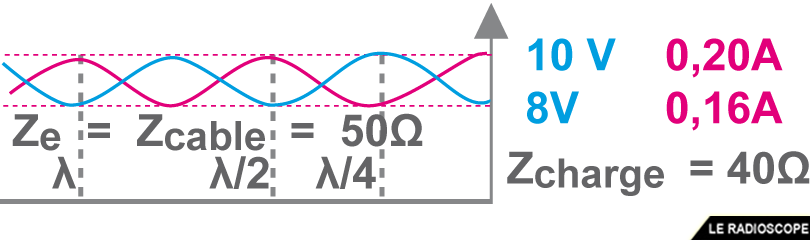
Reprenons le schéma ROS/TOS de l’exemple précédent, à λ/4 de la charge, on a :
• Zλ/4 = U / I = 10V / 0,16A = 62,5Ω
• on peut vérifier que Zcâble² = Zλ/4 x Zcharge :
- 62,5 x 40 = 2500 = 50²
• le phénomène se répète à 3λ/4 de la charge et tous les multiples impairs de quart d’onde
à λ/2 de la charge, on a Zλ/2 = Zcharge
• pas d’incidence de l’affaiblissement linéique du câble sur l’impédance (I et U diminuent dans les mêmes proportions)
• le phénomène se répète à λ et à toutes les demi-ondes
Une ligne quart d’onde pourra être utilisée pour adapter des impédances
• attention à la vélocité du câble pour calculer sa longueur
• ne fonctionne que pour une bande de fréquence
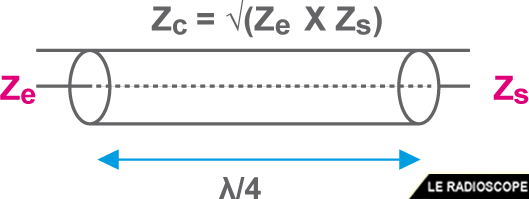
Les propriétés des lignes quart d’onde et demi-onde permettent de réaliser des filtres en insérant des morceaux de câble coaxial (ou de ligne bifilaire) de longueur λ/4 ou λ/2 dans une ligne de transmission.

Balun = BALanced–UNbalanced (symétriseur)
BALUN 1/1
pour rendre symétrique une antenne qui ne l’est pas ou ne l’est plus (symétriseur de tension)

BALUN 1/9
Dit "adaptateur miracle", mais tout est relatif...
CHOKE BALUN
Ce n'est pas un symétriseur de courant
Son nom vient de to choke = étouffer
Autres systèmes d’adaptation :
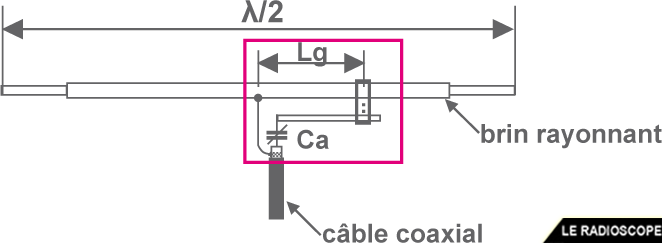
• gamma match
Gamma = Γ
Ajustement avec la longueur du gamma et la valeur de C
Autres systèmes de filtrage/couplage :
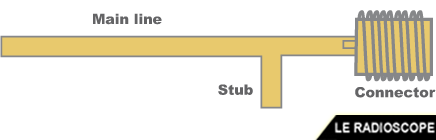
Stub : système apparenté aux lignes d’adaptation quart d’onde/demi-onde
• morceau de ligne de transmission en dérivation sur la ligne principale (à droite : stub en strip-line)
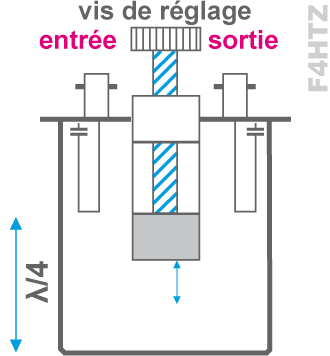
Cavité : couplage de paires d'émetteurs et/ou de récepteurs sur une seule antenne
• montage en série (passe bande)
• ou en dérivation vers la masse (réjecteur)